已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)若函数y=f(x)的图象与直线y= x+a没有交点,求a的取值范围;
x+a没有交点,求a的取值范围;
(3)若函数h(x)=4f(x)+{\;}^{\frac{1}{2}}x+m•2x﹣1,x∈[0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
(必做题)在正方体 中,如图E、F分别是
中,如图E、F分别是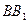 ,CD的中点,
,CD的中点,
(1)求证: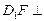 平面ADE;(2)cos
平面ADE;(2)cos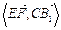 .
.
(本题满分16分)已知圆O: 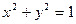 ,圆C:
,圆C: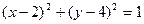 ,由两圆外一点
,由两圆外一点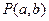 引两圆切线PA、PB,切点分别为A、B,满足|PA|="|PB|." (1)求实数a、b间满足的等量关系;(2)求切线长|PA|的最小值;(3)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.
引两圆切线PA、PB,切点分别为A、B,满足|PA|="|PB|." (1)求实数a、b间满足的等量关系;(2)求切线长|PA|的最小值;(3)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.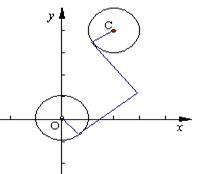
(本题满分13分)已知函数: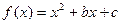 ,其中:
,其中: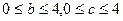 ,且
,且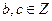 ,记函数
,记函数 满足条件:
满足条件: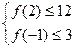 的事件为A,求事件A发生的概率。
的事件为A,求事件A发生的概率。
已知函数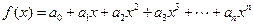 (n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(2)当n为奇函数时,设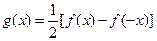 ,是否存在自然数m和M,使不等式m<
,是否存在自然数m和M,使不等式m<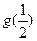 <M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
<M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
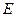 、
、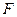 是椭圆
是椭圆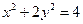 的左、右焦点,
的左、右焦点,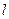 是椭圆的右准线,点
是椭圆的右准线,点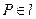 ,过点
,过点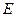 的直线交椭圆于
的直线交椭圆于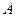 、
、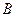 两点.(1)当
两点.(1)当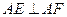 时,求
时,求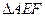 的面积;(2)当
的面积;(2)当 时,求
时,求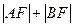 的大小;(3)求
的大小;(3)求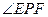 的最大值.
的最大值.