如图,矩形ABCD中,|AB|=2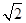 ,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知
,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知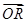 =λ
=λ ,
,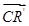 =λ
=λ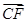 ,其中0<λ<1.
,其中0<λ<1.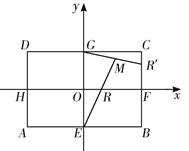
(1)求证:直线ER与GR′的交点M在椭圆Γ: +y2=1上;
+y2=1上;
(2)若点N是直线l:y=x+2上且不在坐标轴上的任意一点,F1、F2分别为椭圆Γ的左、右焦点,直线NF1和NF2与椭圆Γ的交点分别为P、Q和S、T.是否存在点N,使得直线OP、OQ、OS、OT的斜率kOP、kOQ、kOS、kOT满足kOP+kOQ+kOS+kOT=0?若存在,求出点N的坐标;若不存在,请说明理由.
甲、乙、丙三人进行乒乓球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结果相互独立,第1局甲当裁判.
,各局比赛的结果相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)用X表示前4局中乙当裁判的次数,求X的分布列和数学期望.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求直线B1C1与平面A1BC1所成角的正弦值;
(2)在线段BC1上确定一点D,使得AD⊥A1B,并求 的值.
的值.
已知数列{an}满足a1>0,an+1=2-|an|,n∈N*.
(1)若a1,a2,a3成等比数列,求a1的值;
(2)是否存在a1,使数列{an}为等差数列?若存在,求出所有这样的a1;若不存在,说明理由.
在锐角△ABC中,角A,B,C的对边分别为a,b,c.已知sin(A-B)=cosC.
(1)若a=3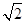 ,b=
,b=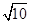 ,求c;
,求c;
(2)求 的取值范围.
的取值范围.