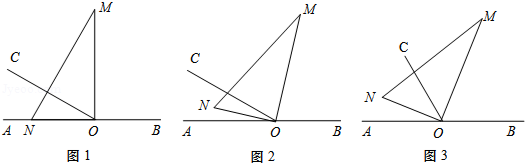
如图1，O为直线AB上一点，过点O作射线OC，∠AOC=30°，将一直角三角板（∠M=30°）的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．
（1）将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．如图2，经过t秒后，OM恰好平分∠BOC．①求t的值；②此时ON是否平分∠AOC？请说明理由；
（2）在（1）问的基础上，若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，如图3，那么经过多长时间OC平分∠MON？请说明理由；
（3）在（2）问的基础上，经过多长时间OC平分∠MOB？请画图并说明理由．
解不等式组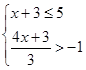
，并求它的整数解.
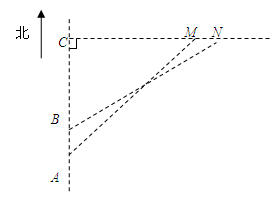
钓鱼岛自古就是中国的领土，中国海监部门已对钓鱼岛及其附属岛屿开展常态化的监视监测.某日，中国一艘海监船从A点沿正北方向巡航，其航线距钓鱼岛（如图，设M、N为改岛的东西两端点）最近的距离为12海里（即MC=12海里）.在A点测得岛屿的西端点M，在点A的东北方向；航行4海里后到达B点，测的岛屿的东端点N在点B的北偏东60°方向（其中M、N、C）在同一直线上，则钓鱼岛东西两端点MN之间的距离为多少海里？（结果精确到0.01海里，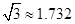
）
某小区准备新建50个停车位，以解决小区停车难的问题．已知新建1个地上停车位和1个地下停车位需0.5万元；新建3个地上停车位和2个地下停车位需1.1万元．
（1）该小区新建1个地上停车位和1个地下停车位各需多少万元？
（2）若该小区预计投资金额超过10万元而不超过11万元，则共有几种建造方案？
在对某地区一次人口抽样统计中，各年龄段的人数如表所示（年龄为整数）．请根据此表回答下列问题：
| 年龄 |
0～9 |
10～19 |
20～29 |
30～39 |
40～49 |
50～59 |
60～69 |
70～79 |
80～89 |
| 人数 |
9 |
11 |
17 |
18 |
17 |
12 |
8 |
6 |
2 |
（1）这次抽样的样本容量是；
（2）在这个样本中，年龄的中位数位于哪个年龄段内；
（3）在这个样本中，年龄在60岁以上（含60岁）的频率是；
（4）如果该地区有人口80 000，为关注人口老龄化问题，请估算该地区60岁以上（含60岁）的人口数．
盒子中有4个球，每个球上写有1～4中的一个数字，不同的球上数字不同．
（1）若从盒中取三个球，以球上所标数字为线段的长，则能构成三角形的概率是多少?
（2）若小明从盒中取出一个球，放回后再取出一个球，然后让小华猜两球上的数字之和，你认为小华猜和为多少时，猜中的可能性大.请说明理由.