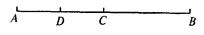在等边 中,

(1)如图1, , 是 边上的两点, , ,求 的度数;
(2)点 , 是 边上的两个动点(不与点 , 重合),点 在点 的左侧,且 ,点 关于直线 的对称点为 ,连接 , .
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点 , 运动的过程中,始终有 ,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明 ,只需证 是等边三角形;
想法2:在 上取一点 ,使得 ,要证明 ,只需证 ;
想法3:将线段 绕点 顺时针旋转 ,得到线段 ,要证 ,只需证 ,
请你参考上面的想法,帮助小茹证明 (一种方法即可).
已知A、B两家商店的随身听的单价相同,书包的单价也相同,随身听和书包的单价之和为452元,且随身听的单价比书包的单价的4倍少8元.
(1)问随身听和书包的单价各是多少元?
(2)现在这两家商店搞促销,促销方式如下:
商店A:所有的商品打八折销售;
商店B:每购物满100元,立即返还25元(例如,购物205元,则立即返还50元).
小明身上带了400元钱,想买随身听和书包各一个,那么,他应该选择在哪一家商店购买更省钱?
如图,OE⊥AB,垂足为O,OF平分∠BOD,∠DOE∶∠EOC=1∶2,求∠AOF的度数.
先化简,再求值: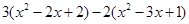 ,其中
,其中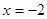 .
.
已知∠A和∠B互余,且∠A=40°30ˊ,求∠B的补角.
如图,线段AB=12cm,C是AB的中点.D是AC的中点,求DB.