如图，是所对弦上一动点，过点作交于点，连接，过点作于点．已知，设、两点间的距离为，、两点间的距离为．（当点与点或点重合时，的值为
小东根据学习函数的经验，对函数随自变量的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了与的几组值，如下表：
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
0 |
2.0 |
2.3 |
2.1 |
|
0.9 |
0 |
（说明：补全表格时相关数值保留一位小数）
（2）建立平面直角坐标系，描出已补全后的表中各对对应值为坐标的点，画出该函数的图象．
（3）结合画出的函数图象，解决问题：当为等腰三角形时，的长度约为 ．
(6分)如图，AB∥CD，CE平分∠ACD，若∠1=25°，求∠2的度数。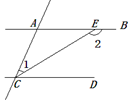
抛物线
交
轴于
、
两点，交
轴于点
，顶点为
.
（1）写出抛物线的对称轴及
、两点的坐标（用含
的代数式表示）（2）连接
并以为直径作⊙
，当
时，请判断⊙是否经过点，并说明理由；（3）在（2）题的条件下，点
是抛物线上任意一点，过作直线垂直于对称轴，垂足为
. 那么是否存在这样的点，使△
与以、、为顶点的三角形相似？若存在，请求出点的坐标；若不存在，请说明理由.
宏达纺织品有限公司准备投资开发A、B两种新产品,通过市场调研发现：如果单独投资A种产品，则所获利润（万元）与投资金额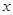
（万元）之间满足正比例函数关系：
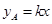；如果单独投资B种产品，则所获利润（万元）与投资金额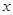（万元）之间满足二次函数关系：
.根据公司信息部的报告，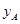
，
（万元）与投资金额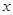（万元）的部分对应值（如下表）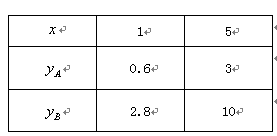
（1）填空：
_______________________；
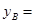_______________________；（2）如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为
（万元），试写出与某种产品的投资金额x之间的函数关系式.（3）请你设计一个在（2）中能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少万元？
如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E.
（1）求证：点E是边BC的中点；
（2）若EC=3，BD=
，求⊙O的直径AC的长度；（3）若以点O，D，E，C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由.
定理：若
、
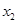是关于
的一元二次方程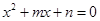
的两实根，则有
，
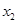.请用这一定理解决问题：已知、是关于的一元二次方程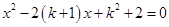
的两实根，且
，求
的值.