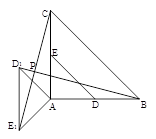
如图,是与弦所围成的图形的内部的一定点,是弦上一动点,连接并延长交于点,连接.已知,设,两点间的距离为,,两点间的距离为,,两点间的距离为.
小腾根据学习函数的经验,分别对函数,随自变量的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量的值进行取点、画图、测量,分别得到了,与的几组对应值;
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
5.62 |
4.67 |
3.76 |
|
2.65 |
3.18 |
4.37 |
|
5.62 |
5.59 |
5.53 |
5.42 |
5.19 |
4.73 |
4.11 |
(2)在同一平面直角坐标系中,描出补全后的表中各组数值所对应的点,,并画出函数,的图象;

(3)结合函数图象,解决问题:当为等腰三角形时,的长度约为 .

如图,已知△ABC.按如下步骤作图: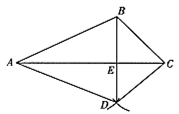
①以A为圆心,AB长为半径画弧;
②以C为圆心,CB长为半径画弧,两弧相交于点D;
③连结BD,与AC交于点E,连结AD,CD.
(1)求证:△ABC≌△ADC;
(2)若∠BAC =30°,∠BCA = 45°,AC = 4,求BE的长.
在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△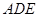 绕点A逆时针旋转,得到等腰Rt△
绕点A逆时针旋转,得到等腰Rt△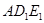 ,设旋转角为
,设旋转角为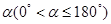 ,记直线
,记直线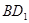 与
与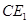 的交点为P.
的交点为P.
(1)如图1,当 时,线段
时,线段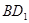 的长等于 ,线段
的长等于 ,线段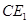 的长等于 ;(直接填写结果)
的长等于 ;(直接填写结果)
(2)如图2,当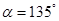 时,求证:
时,求证: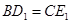 ,且
,且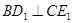 ;
;
(3)①设BC的中点为M,则线段PM的长为 ;②点P到AB所在直线的距离的最大值为 .(直接填写结果)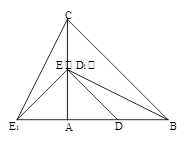
如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.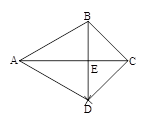
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.
小丽为了测旗杆AB的高度,小丽眼睛距地图1.5米,小丽站在C点,测出旗杆A的仰角为30o,小丽向前走了10米到达点E,此时的仰角为60o,求旗杆的高度。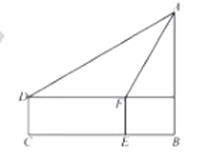
如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC与Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm.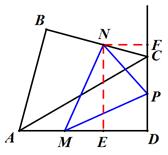
(1)填空:AD= (cm),DC= (cm);
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B的方向运动,当N点运动 到B点时,M,N两点同时停止运动,连结MN,求当M,N点运动了x秒时,点N到AD的距离(用含x的式子表示);
(3)在(2)的条件下,取DC中点P,连结MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出这个最大值.
(参考数据:sin75°=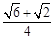 ,sin15°=
,sin15°=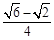 )
)