观察以下等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,
第5个等式:,
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第个等式: (用含的等式表示),并证明.
计算或化简:(本小题共5小题,第(1)3分其余每小题4分,共19分)
(1)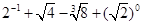
(2) (3)
(3)
(4)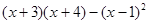 ;(5)
;(5) ÷
÷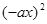 .
.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究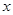 轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: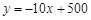 .
.
(1)设李明每月获得利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(不需求出利润的最大值)
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
已知 是⊙
是⊙ 的直径,
的直径,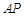 是⊙
是⊙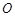 的切线,
的切线,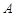 是切点,
是切点, 与⊙
与⊙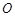 交于点
交于点 .
.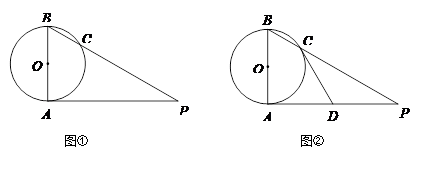
(1)如图①,若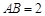 ,
, ,求
,求 的长(结果保留根号);
的长(结果保留根号);
(2)如图②,若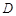 为
为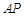 的中点,求证:直线
的中点,求证:直线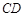 是⊙
是⊙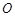 的切线.
的切线.
(1)用配方法把二次函数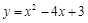 化为顶点式,并在直角坐标系中画出它的大致图象(
化为顶点式,并在直角坐标系中画出它的大致图象( ).
).
(2)若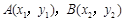 是函数
是函数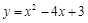 图象上的两点,且
图象上的两点,且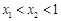 ,请比较
,请比较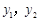 的大小关系.(直接写结果)
的大小关系.(直接写结果)
(3)把方程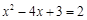 的根在函数
的根在函数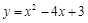 的图象上表示出来.
的图象上表示出来.