一次函数与二次函数的图象的一个交点坐标为,另一个交点是该二次函数图象的顶点.
(1)求,,的值;
(2)过点,且垂直于轴的直线与二次函数的图象相交于,两点,点为坐标原点,记,求关于的函数解析式,并求的最小值.
(1)已知:如图1,在Rt△ABC中,∠C=90°,BC=4,tanB= .求sinA的值.
.求sinA的值.
(2)已知:如图2,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA.求证:△ADE≌△BCE;
(1)解不等式组: (2)化简:
(2)化简:
如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由
请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答:
习题如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.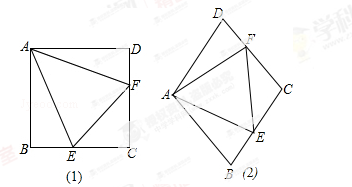
解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,
∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.
∴∠E′AF=90°﹣45°=45°=∠EAF,
又∵AE′=AE,AF=AF
∴△AE′F≌△AEF(SAS)
∴EF=E′F=DE′+DF=BE+DF.
习题研究
观察分析:观察图(1),由解答可知,该题有用的条件是①ABCD是四边形,点E、F分别在边BC、CD上;②AB=AD;③∠B=∠D=90°;④∠EAF=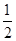 ∠BAD.
∠BAD.
类比猜想:(1)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B=∠D时,还有EF=BE+DF吗?
研究一个问题,常从特例入手,请同学们研究:如图13(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?
(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=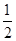 ∠BAD时,EF=BE+DF吗?
∠BAD时,EF=BE+DF吗?
归纳概括:反思前面的解答,思考每个条件的作用,可以得到一个结论“EF=BE+DF”的一般命题:.
山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表: