甲、乙两车分别从、两地同时出发，甲车匀速前往地，到达地立即以另一速度按原路匀速返回到地；乙车匀速前往地，设甲、乙两车距地的路程为（千米），甲车行驶的时间为（时，与之间的函数图象如图所示．
（1）求甲车从地到达地的行驶时间；
（2）求甲车返回时与之间的函数关系式，并写出自变量的取值范围；
（3）求乙车到达地时甲车距地的路程．
已知点P为线段AB的黄金分割点（AP>BP）,且AB=2，求BP的长．
如图，在直角坐标系中，点A的坐标为(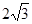
，0)，连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB．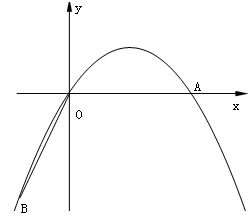
（1）请直接写出点B的坐标；
（2）求经过A、O、B三点的抛物线的解析式；
（3）如果点P是（2）中的抛物线上的动点，且在x轴的上方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．
已知，△ABC为等边三角形，点P是射线CM上一点，连接AP，把△ACP绕点A按顺时针方向旋转60°，得△ABD，直线BD与射线CM交于点E，连接AE.
（1）如图，①求∠BEC的度数；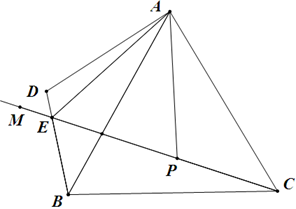
②若AE=2BE，猜想线段CE、BE的数量关系，并证明你的猜想；
（2）如图，若AE=mBE，求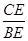
的值．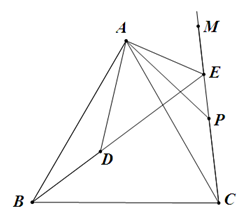
如图，在△ABC中，∠C＝90°，∠A＝30°，AC＝6，点P是线段AC上的一动点，作PD⊥AC，垂足为P，交AB于点D，设AP＝t（0<t<6）．设△APD关于直线PD的对称的图形与四边形BCPD重叠部分的面积为S．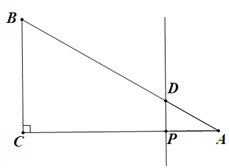
⑴点A关于直线PD的对称点A′与点C重合时，t ＝________；
⑵求S与t的函数关系式．
某文具店销售一种进价为10元/个的签字笔，物价部门规定这种签字笔的售价不得高于14元/个，根据以往经验：以12元/个的价格销售，平均每周销售签字笔100个；若每个签字笔的销售价格每提高1元，则平均每周少销售签字笔10个. 设销售价为x元/个.
（1）该文具店这种签字笔平均每周的销售量为个（用含x的式子表示）；
（2）求该文具店这种签字笔平均每周的销售利润w（元）与销售价x（元/个）之间的函数关系式；
（3）当x取何值时，该文具店这种签字笔平均每周的销售利润最大？最大利润是多少元？