在一个不透明的口袋中装有 1 个红球, 1 个绿球和 1 个白球, 这 3 个球除颜色不同外, 其它都相同, 从口袋中随机摸出 1 个球, 记录其颜色 . 然后放回口袋并摇匀, 再从口袋中随机摸出 1 个球, 记录其颜色, 请利用画树状图或列表的方法, 求两次摸到的球都是红球的概率 .
如图, 是等边三角形,⊙O过点B,C,且与
是等边三角形,⊙O过点B,C,且与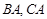 的延长线分别交于点D,E.弦
的延长线分别交于点D,E.弦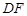 ∥
∥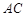 ,
,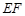 的延长线交
的延长线交 的延长线于点G.
的延长线于点G.
(1)求证: 是等边三角形;
是等边三角形;
(2)若 ,
, ,求
,求 的长.
的长.
光明农场现有某种植物10 000kg,打算全部用于生产高科技药品和保健食品.若生产高科技药品,1kg该植物可提炼出0.01kg的高科技药品,将产生污染物0.1kg;若生产保健食品,1kg该植物可制成0.2kg的保健食品,同时产生污染物0.04kg.已知每生产1kg高科技药品可获利润5 000元,每生产1kg保健食品可获利润100元.要使总利润不低于410 000元,所产生的污染物总量不超过880kg,求用于生产高科技药品的该植物重量的范围.
如图,在 的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
(1)从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为 ;
;
(2)以(1)中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数;
(3)以(1)中的AB为边的两个凸多边形,使它们都是中心对称图形且不全等,其顶点在格点上,各边长都是无理数.
今年“五一黄金周”期间,花果山风景区共接待游客约22.5万人.为了了解该景区的服务水平,有关部门从这些游客中随机抽取450人进行调查,请他们对景区的服务质量进行评分,评分结果的统计数据如下表:
| 档 次 |
第一档 |
第二档 |
第三档 |
第四档 |
第五档 |
| 分值a |
a≥90 |
80≤a<90 |
70≤a<80 |
60≤a<70 |
a<60 |
| 人 数 |
73 |
147 |
122 |
86 |
22 |
根据表中提供的信息,回答下列问题:
(1)所有评分数据的中位数应在第几档内?
(2)若评分不低于70分为“满意”,试估计今年“五一黄金周”期间对花果山景区服务“满意”的游客人数.
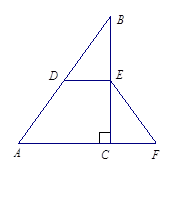
如图,在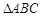 中,
中,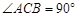 ,
,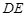 是
是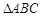 的中位线,点
的中位线,点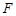 在
在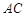 延长上,且
延长上,且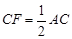 .求证:四边形
.求证:四边形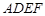 是等腰梯形.
是等腰梯形.