如图,在 的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
(1)从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为 ;
;
(2)以(1)中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数;
(3)以(1)中的AB为边的两个凸多边形,使它们都是中心对称图形且不全等,其顶点在格点上,各边长都是无理数.
为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调查结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
|
课程 |
人数 |
所占百分比 |
|
声乐 |
14 |
|
|
舞蹈 |
8 |
|
|
书法 |
16 |
|
|
摄影 |
|
|
|
合计 |
|
|
根据以上信息,解答下列问题:
(1) , .
(2)求出 的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.

已知:在 外分别以 , 为边作 与 .
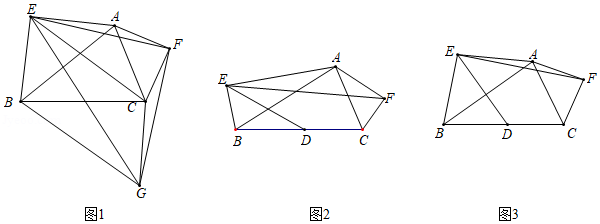
(1)如图1, 与 分别是以 , 为斜边的等腰直角三角形,连接 .以 为直角边构造 ,且 ,连接 , , .
求证:① .
②四边形 是平行四边形.
(2)小明受到图1的启发做了进一步探究:
如图2,在 外分别以 , 为斜边作 与 ,并使 ,取 的中点 ,连接 , 后发现,两者间存在一定的数量关系且夹角度数一定,请你帮助小明求出 的值及 的度数.
(3)小颖受到启发也做了探究:
如图3,在 外分别以 , 为底边作等腰三角形 和等腰三角形 ,并使 ,取 的中点 ,连接 , 后发现,当给定 时,两者间也存在一定的数量关系且夹角度数一定,若 , ,请你帮助小颖用含 , 的代数式直接写出 的值,并用含 的代数式直接表示 的度数.
某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为 元,平均月销售量为 件.
(1)求出 与 的函数关系式,并写出自变量 的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
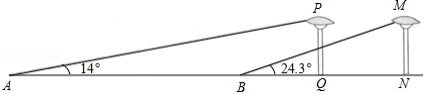
如图,在某街道路边有相距 、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面 处测得路灯 的顶端仰角为 ,向前行走 到达 处,在地面测得路灯 的顶端仰角为 ,已知点 , , , 在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到 .参考数据: , , , , ,
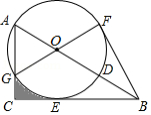
如图,在 中, ,点 在 上,以 为直径的 与边 相切于点 ,与边 相交于点 ,且 ,连接 并延长交 于点 ,连接 .
(1)求证:
① .
② 是 的切线.
(2)若 ,求图形中阴影部分的面积.