某班"数学兴趣小组"对函数 的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量 的取值范围是全体实数, 与 的几组对应值列表如下:
|
|
|
|
|
|
0 |
1 |
2 |
|
3 |
|
|
|
3 |
|
|
|
0 |
|
0 |
|
3 |
|
其中, .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与 轴有 个交点,所以对应的方程 有 个实数根;
②方程 有 个实数根;
③关于 的方程 有4个实数根时, 的取值范围是 .
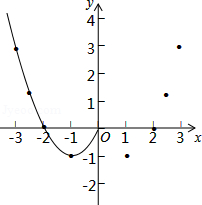
为了解学生的身高情况,抽测了某校17岁的50名男生的身高.数据如下(单位:米):
| 身高 |
1.57 |
1.59 |
1.60 |
1.62 |
1.63 |
1.64 |
1.65 |
1.66 |
1.68 |
| 人数 |
1 |
1 |
2 |
2 |
3 |
2 |
1 |
6 |
5 |
| 身高 |
1.69 |
1.70 |
1.71 |
1.72 |
1.73 |
1.74 |
1.75 |
1.76 |
1.77 |
| 人数 |
8 |
7 |
2 |
3 |
2 |
1 |
2 |
1 |
1 |
若将数据分成7组,取组距为0.03米,相应的频率分布表是:
| 分组 |
频数 |
频率 |
| 1.565~1.595 |
2 |
0.04 |
| 1.595~1.625 |
4 |
0.08 |
| 1.625~1.655 |
6 |
0.12 |
| 1.655~1.685 |
11 |
0.22 |
| 1.685~1.715 |
17 |
0.34 |
| 1.715~1.745 |
6 |
0.12 |
| 1.745~1.775 |
4 |
0.08 |
| 合计 |
50 |
1 |
请回答下列问题:
(1)样本数据中,17岁男生身高的众数、中位数分别是多少?
(2)依据样本数据,估计这所学校17岁的男生中,身高不低于1.65米且不高于1.70米的学生所占的百分比;
(3)观察频率分布表,指出该校17岁的男生中,身高在哪个数据范围内的频率最大.如果该校17岁的男生共有350人,那么在这个身高范围内的人数估计有多少人?
甲、乙两名车工都加工要求尺寸是直径10毫米的零件.从他们所生产的零件中,各取5件,测得直径如下(单位:毫米)
甲:10.05, 10.02,9.97,9.95,10.01
乙:9.99,10.02,10.02,9.98,10.01
分别计算两组数据的标准差(精确到0.01),说明在尺寸符合规格方面,谁做得较好?
在一次家庭年收入的调查中,抽查了15个家庭的年收入(单位:万元)如下表所示:
| 家庭个数 |
每个家庭的年收入 |
| 1 |
0.9 |
| 3 |
1.0 |
| 3 |
1.2 |
| 1 |
1.2 |
| 3 |
1.4 |
| 3 |
1.6 |
| 1 |
18.2 |
根据表中提供的信息,填空:
(1)样本的平均数x=________万元;
(2)样本的中位数=________万元;
(3)样本的标准差σ=________万元(结果保留到小数点后第一位).
(4)你认为在平均数和中位数中,哪一个更能描述这个样本的集中趋势?为什么?
如图,四边形ABCD中,点E在边CD上,连结AE、BE.给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.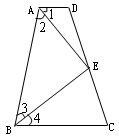
⑴用序号写出一个真命题(书写形式如:如果×××,那么××);并给出证明;
⑵用序号再写出三个真命题(不要求证明)
如图,在等腰梯形ABCD中,AB∥CD,AC、BD是对角线,将△ABD沿AB向下翻折到△ABE的位置,试判定四边形AEBC的形状,并证明你的结论. 