某校七、八年级各有学生400人,为了解这两个年级普及安全教育的情况,进行了抽样调查,过程如下
选择样本,收集数据从七、八年级各随机抽取20名学生,进行安全教育考试,测试成绩(百分制)如下:
七年级 85 79 89 83 89 98 68 89 79 59
99 87 85 89 97 86 89 90 89 77
八年级 71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
分组整理,描述数据
(1)按如下频数分布直方图整理、描述这两组样本数据,请补全八年级20名学生安全教育频数分布直方图;

解析数据,计算填空
(2)两组样本数据的平均数、中位数、众数、优秀率如下表所示,请补充完整;
年级 |
平均数 |
中位数 |
众数 |
优秀率 |
七年级 |
85.3 |
88 |
89 |
|
八年级 |
85.4 |
|
|
|
得出结论,说明理由.
(3)估计八年级成绩优秀的学生人数约为 人.
(4)整体成绩较好的年级为 ,理由为 (至少从两个不同的角度说明合理性).
甲乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.
(1 )A、B两地的距离 千米;乙车速度是 ;a表示 .
(2)乙出发多长时间后两车相距330千米?
齐齐哈尔市教育局非常重视学生的身体健康状况,为此在体育考试中对部分学生的立定跳远成绩进行了调查(分数为整数,满分100分),根据测试成绩(最低分为53分)分别绘制了如下统计表和统计图.(如图)
| 分数 |
59.5分以下 |
59.5分以上 |
69.5分以上 |
79.5以上 |
89.5以上 |
| 人数 |
3 |
42 |
32 |
20 |
8 |
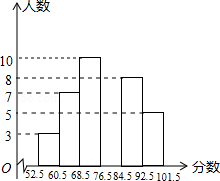
(1)被抽查的学生为 人.
(2)请补全频数分布直方图.
(3)若全市参加考试的学生大约有4500人,请估计成绩优秀的学生约有多少人?(80分及80分以上为优秀)
(4)若此次测试成绩的中位数为78分,请直接写出78.5~89.5分之间的人数最多有多少人?.
如图,已知二次函数y=ax2+bx+c的图象经过点A(﹣4,0),B(﹣1,3),C(﹣3,3)
(1)求此二次函数的解析式;
(2)设此二次函数的对称轴为直线l,该图象上的点P(m,n)在第三象限,其关于直线l的对称点为M,点M关于y轴的对称点为N,若四边形OAPN的面积为20,求m、n的值.
如图所示,在△OAB中,点B的坐标是(0,4),点A的坐标是(3,1).
(1)画出△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1
(2)画出△OAB绕点O逆时针旋转90°后的△OA2B2,并求出点A旋转到A2所经过的路径长(结果保留π)
先化简,再求值: ,其中a、b满足式子
,其中a、b满足式子 .
.