图1是一台实物投影仪,图2是它的示意图,折线表示固定支架,垂直水平桌面于点,点为旋转点,可转动,当绕点顺时针旋转时,投影探头始终垂直于水平桌面,经测量:,,,.(结果精确到.
(1)如图2,,.
①填空: .
②求投影探头的端点到桌面的距离.
(2)如图3,将(1)中的向下旋转,当投影探头的端点到桌面的距离为时,求的大小.
(参考数据:,,,

如图,抛物线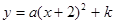 与x轴交于A,0两点,将抛物线向上移动4个单位长度后得到一条新抛物线,它的顶点在x轴上,新抛物线上的D,E两点分别是A,O两点平移后的对应点。设两条抛物线、线段AD和线段OE围成的面积为S。P(m,n)是新抛物线上一个动点,切满足
与x轴交于A,0两点,将抛物线向上移动4个单位长度后得到一条新抛物线,它的顶点在x轴上,新抛物线上的D,E两点分别是A,O两点平移后的对应点。设两条抛物线、线段AD和线段OE围成的面积为S。P(m,n)是新抛物线上一个动点,切满足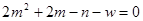
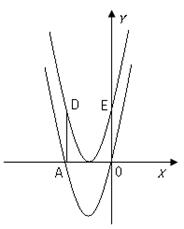
⑴求新抛物线的解析式。
⑵当m=-2时,点F的坐标为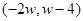 ,试判断直线DF与AE的位置关系,并说明理由。
,试判断直线DF与AE的位置关系,并说明理由。
⑶当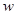 的值最小时,求△AEP的面积与S的数量关系。
的值最小时,求△AEP的面积与S的数量关系。
如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4: 3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求出这个最大面积S。
在梯形ABCD中,DC∥AB,DE⊥AB于点E。
阅读理解:在图一中,延长梯形ABCD的两腰AD,BC交于点P,过点D作DF∥CB交AB于点F,得到图二;四边形BCDF的面积为S,△ADF的面积为S1,△PDC的面积为S2。
解决问题: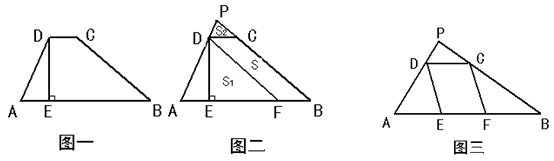
⑴在图一中,若DC=2,AB=8,DE=3,则S =,S1 =,S2 =,则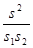 =。
=。
⑵在图二中,若AB=a,DC=b,DE=h,则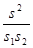 =,并写出理由。
=,并写出理由。
拓展应用:如图三,现有一块地△PAB需进行美化,□DEFC的四个顶点在△PAB的三边上,且种植茉莉花;若△PDC,△ADE,△CFB的面积分别为2m2,3 m2,5 m2且种植月季花。已知1 m2茉莉花的成本为120元,1 m2月季的成本为80元。试利用⑵中的结论求□DEFC的面积,并求美化后的总成本是多少元?
已知某种水果的批发单价与批发量的函数关系如图1所示:
⑴请说明图中①②两段函数图象的实际意义。
⑵写出批发该种水果的资金金额w元与批发量m kg之间的函数关系式;在图2的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果。
⑶经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系式如图3所示,该经销商以每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日的利润最大。
某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?