某市为了创建绿色生态城市,在城东建了"东州湖"景区,小明和小亮想测量"东州湖"东西两端 、 间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点 的一点 ,并测得 米,点 位于点 的北偏西 方向,点 位于点 的北偏东 方向.
请你根据以上提供的信息,计算"东州湖"东西两端之间 的长.(结果精确到1米)
(参考数据: , , , .

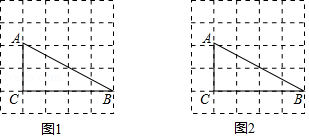
如图,在 的网格中, 的三个顶点都在格点上.
(1)在图1中画出一个以 为边的 ,使顶点 , 在格点上.
(2)在图2中画出一条恰好平分 周长的直线 (至少经过两个格点).
先化简,再求值: ,其中 .
计算: .
定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

【基础巩固】
(1)如图1,在 中, 为 上一点, .求证: .
【尝试应用】
(2)如图2,在 中, 为 上一点, 为 延长线上一点, .若 , ,求 的长.
【拓展提高】
(3)如图3,在菱形 中, 是 上一点, 是 内一点, , , , , ,求菱形 的边长.
