某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了"望月阁"及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量"望月阁"的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与"望月阁"底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:如图,小芳在小亮和"望月阁"之间的直线 上平放一平面镜,在镜面上做了一个标记,这个标记在直线 上的对应位置为点 ,镜子不动,小亮看着镜面上的标记,他来回走动,走到点 时,看到"望月阁"顶端点 在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度 米, 米,然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从 点沿 方向走了16米,到达"望月阁"影子的末端 点处,此时,测得小亮身高 的影长 米, 米.
如图,已知 , , ,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出"望月阁"的高 的长度.

已知格点△ABC.
(1)画出与△ABC相似的格点△A1B1C1,使△A1B1C1与△ABC的相似比为2;
(2)画出与△ABC相似的格点△A2B2C2,使△A2B2C2与△ABC的相似比为 ;
;
(3)格点△A1B1C1和格点△A2B2C2的相似比为 .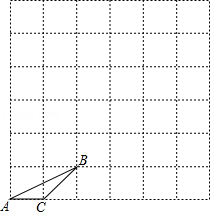
今年3月5日,我校组织全体学生参加了“走出校门,服务社会”的活动.九年级三班同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图.请根据同学所作的两个图形.解答:
(1)九年级三班有多少名学生;
(2)补全直方图的空缺部分;
(3)若九年级有800名学生,估计该年级去敬老院的人数.
如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为6个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)图中如果点A、B表示的数是互为相反数,那么点A表示的数是 ;
(2)当t=2秒时,点A与点P之间的距离是 个长度单位;
(3)当点A为原点时,点P表示的数是 ;(用含t的代数式表示)
(4)当t= 秒时,点P到点A的距离是点P到点B的距离的2倍.
自从有了用字母表示数,我们发现表达有关的数和数量关系更加的简洁明了,从而更助于发现更多有趣的结论,请你按要求试一试:
(1)填空:
①32﹣22= ;(3+2)×(3﹣2)= ;
②22﹣52= ;(2+5)×(2﹣5)= ;
(2)猜一猜:a2﹣b2与(a+b)(a﹣b)的大小关系是 ;
(3)利用你发现的结论,算一算:20152﹣20172.
据报道,受台风“杜鹃”影响,2015年9月27日我县瓯江的水位是2.3米.下表是该地区9月28日至10月3日的水位变化情况(单位:m):
| 日期 |
28 |
29 |
30 |
1 |
2 |
3 |
| 水位记录 |
+0.7 |
+0.4 |
﹣0.9 |
﹣0.6 |
+0.1 |
﹣0.3 |
注:规定水位比前一天上升用“+”,比前一天下降用“﹣”,不升不降用“0”.
(1)该地区这6天内水位最高的一天是 日,实际水位是 米;
(2)与9月27日相比,10月3日该地区水位是上升了,还是下降了?变化了多少?