问题提出
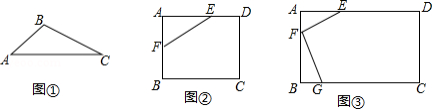
(1)如图①,已知 ,请画出 关于直线 对称的三角形.
问题探究
(2)如图②,在矩形 中, , , , ,是否在边 、 上分别存在点 、 ,使得四边形 的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决
(3)如图③,有一矩形板材 , 米, 米,现想从此板材中裁出一个面积尽可能大的四边形 部件,使 , 米, ,经研究,只有当点 、 、 分别在边 、 、 上,且 ,并满足点 在矩形 内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形 部件?若能,求出裁得的四边形 部件的面积;若不能,请说明理由.
在平面直角坐标系中,抛物线
 与x轴的两个交点分别为A(-3,0),B
与x轴的两个交点分别为A(-3,0),B
(1,0),过顶点C作CH⊥x轴于点H.
(1)a=,b=,顶点C的坐标为.
(2)在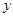 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.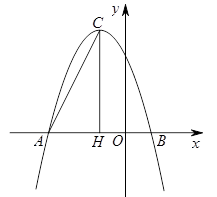
如图,将边长为4的等边三角形AOB放置于平面直角坐标系xOy中,F是AB边上的动点(不与点A,B重合),过点F的反比例函数 (
( ,
, )与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
)与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.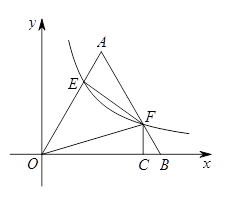
(1)若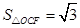 ,求反比例函数的解析式.
,求反比例函数的解析式.
(2)在(1)的条件下,试判断以点E为圆心,EA长为半径的圆与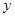 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.
(3)AB边上是否存在点F,使得EF⊥AE?若存在,请求出BF:FA的值;若不存在,请说明理由.
铜陵学院毕业生小张响应国家“自主创业”的号召,投资开办了一个装饰品商店,该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件。销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系: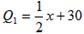 (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数)。
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数)。
(1)第25天该商店的日销售利润为多少元?
(2)试写出该商店日销售利润y(元)关于销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润。
为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,二中学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间,根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题: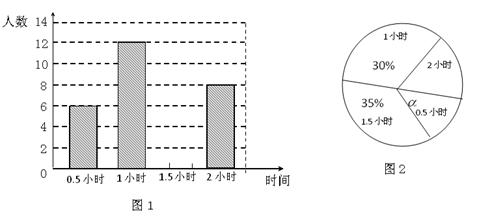
(1)本次调查的学生人数是人.
(2)图2中α是度,并将图1条形统计图补充完整.
(3)请估算该校九年级学生自主学习的时间不少于1.5小时有人.
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).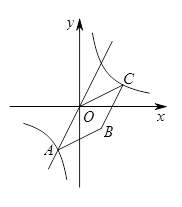
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移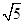 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.