在平面直角坐标系中,抛物线
 与x轴的两个交点分别为A(-3,0),B
与x轴的两个交点分别为A(-3,0),B
(1,0),过顶点C作CH⊥x轴于点H.
(1)a= ,b= ,顶点C的坐标为 .
(2)在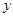 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.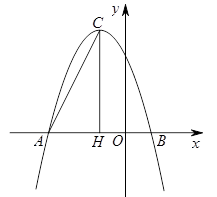
某港受潮汐的影响,近日每天24小时港内的水深变化大体如下图: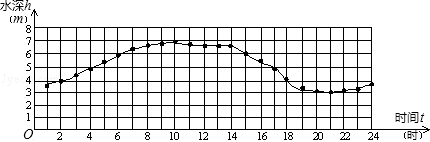
一般货轮于上午7时在该港码头开始卸货,计划当天卸完货后离港.已知这艘货轮卸完货后吃水深度为2.5m(吃水深度即船底离开水面的距离).该港口规定:为保证航行安全,只有当船底与港内水底间的距离不少于3.5m时,才能进出该港.
根据题目中所给的条件,回答下列问题:
(1)要使该船能在当天卸完货并安全出港,则出港时水深不能少于 m,卸货最多只能用 小时;
(2)已知该船装有1200吨货,先由甲装卸队单独卸,每小时卸180吨,工作了一段时间后,交由乙队接着单独卸,每小时卸120吨.如果要保证该船能在当天卸完货并安全出港,则甲队至少应工作几小时,才能交给乙队接着卸?
某海产品市场管理部门规划建造面积为2400m2的集贸大棚,大棚内设A种类型和B种类型的店面共80间,每间A种类型的店面的平均面积为28m2,月租费为400元;每间B种类型的店面的平均面积为20m2,月租费为360元.全部店面的建造面积不低于大棚总面积的80%,又不能超过大棚总面积的85%.
(1)试确定A种类型店面的数量的范围;
(2)该大棚管理部门通过了解业主的租赁意向得知,A种类型店面的出租率为75%,B种类型店面的出租率为90%.
①开发商计划每年能有28万元的租金收入,你认为这一目标能实现吗?若能,应该如何安排A、B两类店面数量?若不能,说明理由.
②为使店面的月租费最高,最高月租金是多少?
如图,在平面直角坐标系中,点A、B分别在x轴y轴的正半轴上,线段OA的长是不等式5x﹣4<3(x+2)的最大整数解,线段OB的长是一元二次方程x2﹣2x﹣3=0的一个根,将Rt△ABO沿BE折叠,使AB边落在OB边所在的y轴上,点A与点D重合.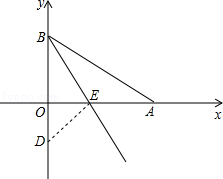
(1)求OA、OB的长;
(2)求直线BE的解析式;
(3)在平面内是否存在点M,使B、O、E、M为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
水果商李老板在高州市收购有香蕉120吨,在海口市收购有香蕉60吨,现要销往北京100吨,沈阳80吨(全部用汽车运输).已知从高州运一吨香蕉到北京和沈阳分别需800元和1000元;从海口运一吨香蕉到北京和沈阳分别需1000元和1300元.
(1)设从海口运往北京x吨,求总运费y(元)关于x(吨)的函数关系式;
(2)李老板计划用17万元开支运费,够用吗?
(3)若每辆车装10吨,且不能浪费车力.李老板要把总运费控制在不超过17.5万元,有多少种调运方案可实现?
(4)请根据前面的要求画出这一函数的图象.
某企业有员工300人生产A种产品,平均每人每年可创造利润m万元(m为大于零的常数).为减员增效,决定从中调配x人去生产新开发的B种产品.根据评估,调配后继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54m万元.
(1)调配后企业生产A种产品的年利润为 万元,生产B种产品的年利润为 万元(用含rn的代数式表示).若设调配后企业全年的总利润为y万元,则y关于x的关系式为 ;
(2)若要求调配后企业生产A种产品的年利润不少于调配前企业年利润的五分之四,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案?请设计出来,并指出其中哪种方案全年总利润最大(必要时运算过程可保留3个有效数字).
(3)企业决定将(2)中的年最大总利润(m=2)继续投资开发新产品,现有六种产品可供选择(不得重复投资同一种产品),各产品所需资金以及所获利润如下表:
| 产 品 |
C |
D |
E |
F |
G |
H |
| 所需资金(万元) |
200 |
348 |
240 |
288 |
240 |
500 |
| 年 利 润(万元) |
50 |
80 |
20 |
60 |
40 |
85 |
如果你是企业决策者,为使此项投资所获年利润不少于145万元,你可以投资开发哪些产品?请你写出两种投资方案.