在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行修整改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜,今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
品种 项目 |
产量(斤每棚) |
销售价(元每斤) |
成本(元每棚) |
香瓜 |
2000 |
12 |
8000 |
甜瓜 |
4500 |
3 |
5000 |
现假设李师傅今年下半年香瓜种植的大棚数为个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为元.
根据以上提供的信息,请你解答下列问题:
(1)求出与之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.
解不等式:3(x-1)+2≥2(x-3).
我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:如图1,在四边形ABCD中,取对角线BD的中点O,连结OA、OC. 显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.
(1)试说明直线AE是“好线”的理由;
(2)如图2,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,只需对画图步骤作适当说明(不需要说明“好线”的理由).
两条相交的直线OX、OY,使∠XOY=nº,在射线OX、OY上分别再任意取A、B两点,作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,随着点A、B位置的变化,∠C的大小是否会变化?若保持不变,请求出∠C的度数;若发生变化,求出变化范围.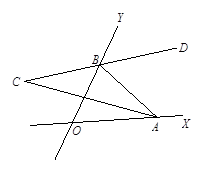
(1)如图,∠MON=80º,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P. 试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围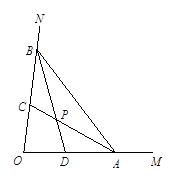
如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.
试判断∠1、∠2的数量关系,并说明理由.
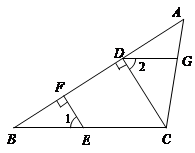 |