小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部,如图所示.于是他们先在古树周围的空地上选择一点,并在点处安装了测量器,测得古树的顶端的仰角为;再在的延长线上确定一点,使米,并在处的地面上水平放置了一个小平面镜,小明沿着方向移动,当移动到点时,他刚好在小平面镜内看到这棵古树的顶端的像,此时,测得米,小明眼睛与地面的距离米,测倾器的高度米.已知点、、、在同一水平直线上,且、、均垂直于,求这棵古树的高度.(小平面镜的大小忽略不计)

(本小题10分)一个半径为 海里的暗礁群中央
海里的暗礁群中央 处建有一个灯塔,一艘货轮由东向西航行,第一次在
处建有一个灯塔,一艘货轮由东向西航行,第一次在 处观测此灯塔在北偏西
处观测此灯塔在北偏西 方向,航行了
方向,航行了 海里后到
海里后到 ,灯塔在北偏西
,灯塔在北偏西 方向,如图.问货轮沿原方向航行有无危险?
方向,如图.问货轮沿原方向航行有无危险?
(本小题10分)如图,已知在 中,
中, 是
是 平分线,点
平分线,点 在
在 边上,且
边上,且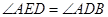 .
.
求证:(1) ∽
∽ ;(2)
;(2) .
.
在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其
中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的
一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,
将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这
个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
(1)求抛物线的函数表达式;
(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①当x取何值时,线段PQ的长度取得最大值,其最大值是多少?
②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66°.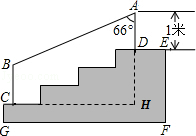
(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度l(即AD+AB+BC,结果精确到0.1米).(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25,cot66°≈0.45)