请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德 ,公元前 公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿拉伯 年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据 译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1, 和 是 的两条弦(即折线 是圆的一条折弦), , 是 的中点,则从 向 所作垂线的垂足 是折弦 的中点,即 .下面是运用"截长法"证明 的部分证明过程.证明:如图2,在 上截取 ,连接 , , 和 .
是 的中点,
.
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边 内接于 , , 为 上一点, , 于点 ,则 的周长是 .
如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少?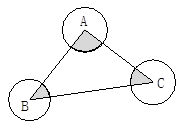
先阅读,再解答:
我们在判断点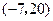 是否在直线
是否在直线 上时,常用的方法:把
上时,常用的方法:把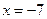 代入
代入 中,由
中,由 ,判断出点
,判断出点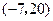 不在直线
不在直线 上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由。
上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由。
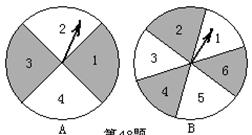
如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏,其规则如下:
⑴同时自由转动转盘A与B;
⑵转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针停留在某一数字为止),用所指的两个数字作乘积,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,那么乙胜(如转盘A指针指向3,转盘B指针指向5,3×5=15,按规则乙胜)。你认为这样的规则是否公平?请说明理由;如果不公平,请你设计一个公平的规则,并说明理由。
解方程: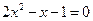 。
。
把下列各数填入表示它所在的数集的大括号:(本小题4分)