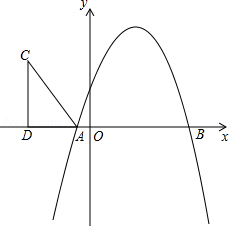
综合与探究如图，在平面直角坐标系中，已知抛物线yax2bx8-优题课

题文

综合与探究

如图，在平面直角坐标系中，已知抛物线 $y = a x^{2} + bx - 8$ 与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴交于点 $C$ ，直线 $l$ 经过坐标原点 $O$ ，与抛物线的一个交点为 $D$ ，与抛物线的对称轴交于点 $E$ ，连接 $CE$ ，已知点 $A$ ， $D$ 的坐标分别为 $(- 2, 0)$ ， $(6, - 8)$ ．

（1）求抛物线的函数表达式，并分别求出点 $B$ 和点 $E$ 的坐标；

（2）试探究抛物线上是否存在点 $F$ ，使 $ΔFOE ≅ ΔFCE$ ？若存在，请直接写出点 $F$ 的坐标；若不存在，请说明理由；

（3）若点 $P$ 是 $y$ 轴负半轴上的一个动点，设其坐标为 $(0, m)$ ，直线 $PB$ 与直线 $l$ 交于点 $Q$ ，试探究：当 $m$ 为何值时， $ΔOPQ$ 是等腰三角形．

科目数学题型解答题难度较难

知识点：二次函数的性质一次函数的性质待定系数法求二次函数解析式全等三角形的判定与性质二次函数综合题等腰三角形的判定与性质

登录免费查看答案和解析

相关试题

当前， “精准扶贫”工作已进入攻坚阶段，凡贫困家庭均要“建档立卡” ．某初级中学七年级共有四个班，已“建档立卡”的贫困家庭的学生人数按一、二、三、四班分别记为 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $A_{4}$ ，现对 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $A_{4}$ 统计后，制成如图所示的统计图．

（1）求七年级已“建档立卡”的贫困家庭的学生总人数；

（2）将条形统计图补充完整，并求出 $A_{1}$ 所在扇形的圆心角的度数；

（3）现从 $A_{1}$ ， $A_{2}$ 中各选出一人进行座谈，若 $A_{1}$ 中有一名女生， $A_{2}$ 中有两名女生，请用树状图表示所有可能情况，并求出恰好选出一名男生和一名女生的概率．

如图，抛物线 $y = - x^{2} + bx + c$ 与 $x$ 轴分别交于 $A (- 1, 0)$ ， $B (5, 0)$ 两点．

（1）求抛物线的解析式；

（2）在第二象限内取一点 $C$ ，作 $CD$ 垂直 $x$ 轴于点 $D$ ，连接 $AC$ ，且 $AD = 5$ ， $CD = 8$ ，将 $Rt Δ ACD$ 沿 $x$ 轴向右平移 $m$ 个单位，当点 $C$ 落在抛物线上时，求 $m$ 的值；

（3）在（2）的条件下，当点 $C$ 第一次落在抛物线上记为点 $E$ ，点 $P$ 是抛物线对称轴上一点．试探究：在抛物线上是否存在点 $Q$ ，使以点 $B$ 、 $E$ 、 $P$ 、 $Q$ 为顶点的四边形是平行四边形？若存在，请求出点 $Q$ 的坐标；若不存在，请说明理由．

如图， $AB$ 是 $⊙ O$ 的直径，点 $C$ 在 $AB$ 的延长线上， $AD$ 平分 $∠ CAE$ 交 $⊙ O$ 于点 $D$ ，且 $AE ⊥ CD$ ，垂足为点 $E$ ．

（1）求证：直线 $CE$ 是 $⊙ O$ 的切线．

（2）若 $BC = 3$ ， $CD = 3 \sqrt{2}$ ，求弦 $AD$ 的长．

如图，一次函数 $y = kx + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于点 $A (- 3, m + 8)$ ， $B (n, - 6)$ 两点．

（1）求一次函数与反比例函数的解析式；

（2）求 $ΔAOB$ 的面积．

如图，为了测量某条河的宽度，现在河边的一岸边任意取一点 $A$ ，又在河的另一岸边取两点 $B$ 、 $C$ 测得 $∠ α = 30 °$ ， $∠ β = 45 °$ ，量得 $BC$ 长为100米．求河的宽度（结果保留根号）．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号