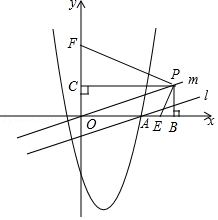
如图:在平面直角坐标系中,直线与轴交于点,经过点的抛物线的对称轴是.
(1)求抛物线的解析式;
(2)平移直线经过原点,得到直线,点是直线上任意一点,轴于点,轴于点,若点在线段上,点在线段的延长线上,连接,,且.求证:;
(3)若(2)中的点坐标为,点是轴上的点,点是轴上的点,当时,抛物线上是否存在点,使四边形是矩形?如果存在,请求出点的坐标,如果不存在,请说明理由.
如图,已知 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交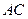 于点
于点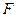 ,点
,点 为
为
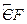 的中点,连接
的中点,连接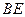 交
交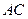 于点
于点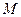 ,
,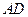 为
为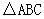 的角平分线,且
的角平分线,且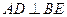 ,垂足为点
,垂足为点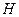 。
。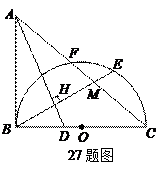
(1)求证: 是半圆
是半圆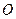 的切线;
的切线;
(2)若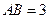 ,
,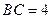 ,求
,求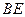 的长。
的长。
如图,抛物线与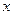 轴交于
轴交于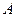 (
(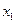 ,0)、
,0)、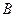 (
(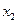 ,0)两点,且
,0)两点,且 ,与
,与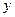 轴交于点
轴交于点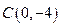 ,其中
,其中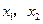 是方程
是方程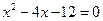 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点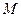 是线段
是线段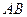 上的一个动点,过点
上的一个动点,过点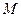 作
作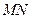 ∥
∥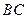 ,交
,交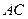 于点
于点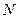 ,连接
,连接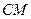 ,当
,当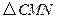 的面积最大时,求点
的面积最大时,求点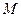 的坐标;
的坐标;
(3)点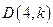 在(1)中抛物线上,点
在(1)中抛物线上,点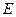 为抛物线上一动点,在
为抛物线上一动点,在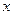 轴上是否存在点
轴上是否存在点 ,使以
,使以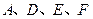 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
如图,已知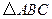 ,以
,以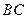 为直径,
为直径,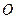 为圆心的半圆交
为圆心的半圆交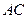 于点
于点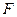 ,点
,点 为
为
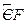 的中点,连接
的中点,连接 交
交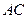 于点
于点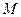 ,
,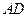 为
为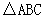 的角平分线,且
的角平分线,且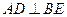 ,垂足为点
,垂足为点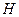 。
。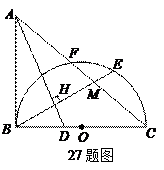
(1)求证: 是半圆
是半圆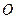 的切线;
的切线;
(2)若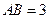 ,
,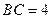 ,求
,求 的长。
的长。
我州鼓苦荞茶、青花椒、野生蘑菇,为了让这些珍宝走出大山,走向世界,州政府决定组织21辆汽车装运这三种土特产共120吨,参加全国农产品博览会。现有A型、B型、C型三种汽车可供选择。已知每种型号汽车可同时装运2种土特产,且每辆车必须装满。根据下表信息,解答问题。
 |
苦荞茶 |
青花椒 |
野生蘑菇 |
||
| 每 辆 汽 车 运 载 量 |
(吨) |
A型 |
 2 2 |
2 |
|
| B型 |
4 |
2 |
|||
| C型 |
1 |
6 |
|||
| 车型 |
A |
B |
C |
| 每辆车运费(元) |
1500 |
1800 |
2000 |
(1)设A型汽车安排 辆,B 型汽车安排
辆,B 型汽车安排 辆,求
辆,求 与
与 之间的函数关系式。
之间的函数关系式。
(2)如果三种型号的汽车都不少于4辆,车辆安排有几种方案?并写出每种方案。
(3)为节约运费,应采用(2)中哪种方案?并求出最少运费。
.在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图, ∥
∥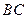 ,坝高10m,迎水坡面
,坝高10m,迎水坡面 的坡度
的坡度 ,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面
,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面 的坡度进行修改,修改后的迎水坡面
的坡度进行修改,修改后的迎水坡面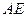 的坡度
的坡度 。
。
(1)求原方案中此大坝迎水坡 的长(结果保留根号)
的长(结果保留根号)
(2)如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿 方向拓宽2.7m,求坝顶将会沿
方向拓宽2.7m,求坝顶将会沿 方向加宽多少米?
方向加宽多少米?