对任意一个三位数,如果满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为.例如,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为,,所以.
(1)计算:,;
(2)若,都是“相异数”,其中,,,,都是正整数),规定:,当时,求的最大值.
为提高初中生的身体素质,教育行政部门规定:初中生每天参加户外活动的平均时间应不少于1小时.为了解学生参加户外活动的情况,某区教育行政部门对部分学生参加户外活动的时间进行了抽样调查,并将调查结果绘制成下列两幅不完整的统计图,请你根据图中提供的信息解答以下问题: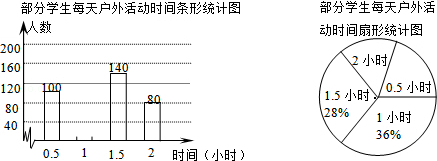
(1)这次抽样共调查了 名学生,并补全条形统计图;
(2)计算扇形统计图中表示户外活动时间0.5小时的扇形圆心角度数;
(3)本次调查学生参加户外活动的平均时间是否符合要求?(写出判断过程)
修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独承包要120天完成。
(1)现由甲、乙两个工程队合作承包,多少天可以完成?
(2)如果甲、乙两工程队合作了30天后,因甲工程队另有任务,剩下的工作由乙工程队完成,则修好这条公路一共需要多少天完成?
(1)关于x的一元一次方程(k2﹣1)xk﹣1+(k﹣1)x﹣8=0的解是:x=
(2)(此应用题横线部分被墨水污染,补全条件,并列出方程)用电脑打印一份书稿,甲需30h,乙需20h,现甲打字3h后. ,列方程得 .
(3)如图,是由几个相同的小立方体搭成的几何体的俯视图,小正方形中数字表示该位置小立方体的个数,按横线部分要求画图.
如图,已知∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC.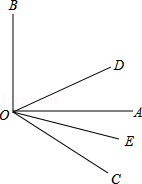
(1)求∠DOE的度数.
(2)如果原题中∠AOC=60°改为∠AOC是锐角,能否求出∠DOE?若能求出来;若不能,说明理由.
先化简,再求值:2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=1,y=﹣1.