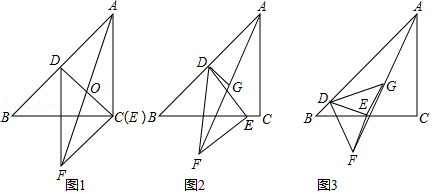
如图，在等腰中，，，点，分别在边，上，将线段绕点按逆时针方向旋转得到．
（1）如图1，若，点与点重合，与相交于点．求证：．
（2）已知点为的中点．
①如图2，若，，求的长．
②若，是否存在点，使得是直角三角形？若存在，求的长；若不存在，试说明理由．
（本小题10分）已知AB，BC，CD分别与⊙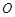
相切于E，F，G三点，且AB∥CD，连接OB，OC．
（1）如图①，求∠BOC的度数；
（2）如图②，延长CO交⊙O于点M，过点M做MN∥OB交CD于点N，当OB=6，OC=8时，求⊙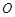的半径及MN的长．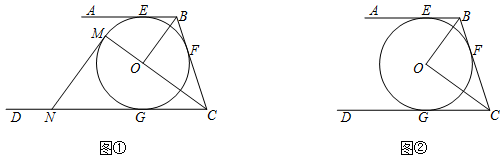
（本小题8分）已知抛物线y=
+bx+c过点（0，0），（1，3），求抛物线的解析式，并求出抛物线的顶点坐标．
（本小题8分）
（1）解方程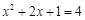
；
（2）利用判别式判断方程
的根的情况．
如图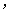
将线段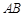
放在每个小正方形的边长为
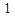的网格中，点
，点
均落在格点上．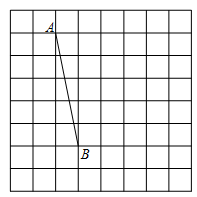
（1）AB的长等于；
（2）请在如图所示的网格中，用无刻度的直尺，在线段AB上画出点P，使
，并简要说明画图方法（不要求证明）．
如图，抛物线y = ax2 + bx + 4与x轴的两个交点分别为A（－4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长及H点的坐标；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．