某旅行团32人在景区游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区游玩.景区的门票价格为100元张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).
(1)这次调查中,一共查了 名学生:
(2)请补全两幅统计图:
(3)若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
先化简,再求值: ,其中a=﹣2.
,其中a=﹣2.
如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.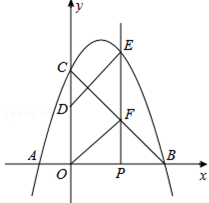
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)