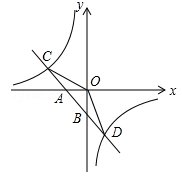
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
(乐山)如图1,二次函数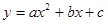 的图象与
的图象与 轴分别交于A、B两点,与
轴分别交于A、B两点,与 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程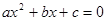 的两根为-8、2.
的两根为-8、2.
(1)求二次函数的解析式;
(2)直线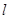 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止, 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结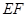 ,求△PEF周长的最小值.
,求△PEF周长的最小值.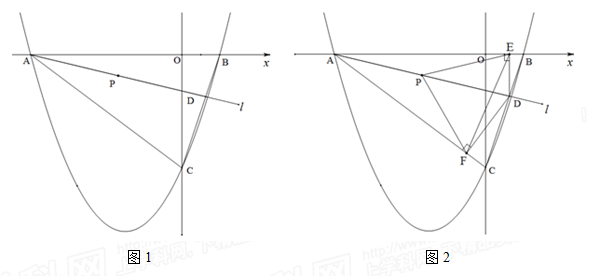
已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.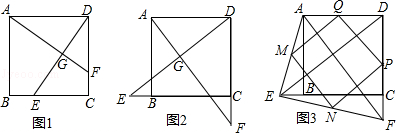
如图,已知抛物线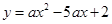 (
(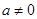 )与y轴交于点C,与x轴交于点A(1,0)和点B.
)与y轴交于点C,与x轴交于点A(1,0)和点B.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件的点N的坐标;若不能,请说明理由.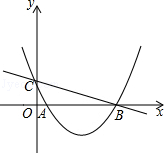
(攀枝花)某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价﹣进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
(攀枝花)如图,已知一次函数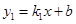 的图象与x轴、y轴分别交于A、B两点,与反比例函数
的图象与x轴、y轴分别交于A、B两点,与反比例函数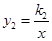 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数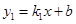 与反比例函数
与反比例函数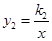 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出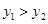 时自变量x的取值范围.
时自变量x的取值范围.