随着5G技术的发展，人们对各类5G产品的使用充满期待，某公司-优题课

题文

随着 $5 G$ 技术的发展，人们对各类 $5 G$ 产品的使用充满期待，某公司计划在某地区销售一款 $5 G$ 产品，根据市场分析，该产品的销售价格将随销售周期的变化而变化．设该产品在第 $x (x$ 为正整数）个销售周期每台的销售价格为 $y$ 元， $y$ 与 $x$ 之间满足如图所示的一次函数关系．

（1）求 $y$ 与 $x$ 之间的关系式；

（2）设该产品在第 $x$ 个销售周期的销售数量为 $p$ （万台）， $p$ 与 $x$ 的关系可以用 $p = \frac{1}{2} x + \frac{1}{2}$ 来描述．根据以上信息，试问：哪个销售周期的销售收入最大？此时该产品每台的销售价格是多少元？

科目数学题型解答题难度中等

知识点：二次函数的应用一次函数的应用

登录免费查看答案和解析

相关试题

把下列各数填入表示它所在的数集的大括号：
－2．4，3，2．008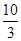，－，0．1010010001…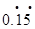，－，0，－（－2．28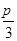），，－|－4|
无理数集合：{…}；
分数集合： {…}；
非正整数集合：{…}；
正数集合：{…}．

（本小题12分）小明有5张写着不同数字的卡片，请按要求抽出卡片，完成下列各问题：

（1）从中取出2张卡片，使这2张卡片上数字的乘积最大，如何抽取？最大值是多少?
答：我抽取的2张卡片是、，乘积的最大值为．
（2）从中取出2张卡片，使这2张卡片上数字相除的商最小，如何抽取？最小值是多少?
答：我抽取的2张卡片是、，商的最小值为．
（3）从中取出4张卡片，用学过的运算方法，使结果为24．如何抽取？写出运算式子．（写出一种即可）
答：我抽取的4张卡片是、、、，
算24的式子为．

（本小题10分）如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（+l，+3）；从C到D记为：C→D（+1，－2）。其中第一个数表示左右方向，第二个数表示上下方向，那么图中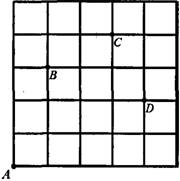

（1）A→C（，），C→ （-2，）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）假如这只甲虫从A处去甲虫P处的行走路线依次为（＋2，＋2），（＋1，－1），（－1，＋3），请在图中标出P的位置．

（本小题10分）（1）观察一列数a₁＝3，a₂＝3²，a₃＝3³，a₄＝3⁴，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是_______；根据此规律，如果a_n（n为正整数）表示这个数列的第n项，那么a₆＝_______，a_n＝_______；（可用幂的形式表示）
（2）如果想要求l＋2＋2²＋2³＋．．．＋2¹⁰的值，可令S₁₀＝l＋2＋2²＋2³＋．．．＋2¹⁰，①将①式两边同乘以2，得_______②，由②减去①式，得S₁₀＝_______．
（3）若（1）中数列共有20项，设S₂₀＝3＋3²＋3³＋3⁴＋…＋a₂₀，请利用上述规律和方法计算S₂₀的值．

（本小题8分）某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶纪录如下．（单位：km）

第一次	第二次	第三次	第四次	第五次	第六次	第七次
－4	＋7	－9	＋8	＋6	－5	－2

（1）求收工时距A地多远？
（2）在第次纪录时距A地最远；
（3）若每km耗油0．3升，问共耗油多少升？

试卷网试题网古诗词网作文网范文网