如图,在正方形中,点是上的一点,点是延长线上的一点,且,连结、、.
(1)求证:;
(2)若,请求出的长.

请你在下面3个网格(两相邻格点的距离均为1个单位长度)内,分别设计1个图案,要求:在图(1)中所设计的图案是面积等于 的轴对称图形;在图(2)中所设计的图案是面积等于2
的轴对称图形;在图(2)中所设计的图案是面积等于2 的中心对称图形;在图(3)中所设计的图案既是轴对称图形又是中心对称图形,并且面积等于3
的中心对称图形;在图(3)中所设计的图案既是轴对称图形又是中心对称图形,并且面积等于3 .将你设计的图案用铅笔涂黑.
.将你设计的图案用铅笔涂黑.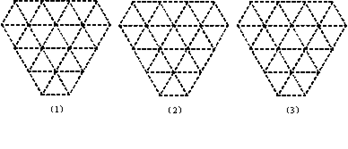
某中学九年级有100名学生参加了数学竞赛.已知竞赛成绩都是整数,试题满分为150分,参赛学生的成绩统计情况如下图: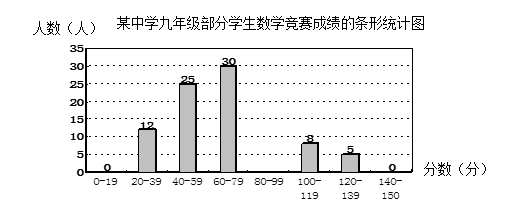
请根据以上信息完成下列问题:
(1)将该统计图补充完整;
(2)竞赛成绩的中位数落在上表中的分数段内;
(3)若80分以上 (含80分)的考生均可获得不同等级的奖励, 该校参加竞赛的学生获奖率为 % 。
如图,Ð1 = Ð2,ÐB = ÐD,AB =" DE" = 5,BC = 4.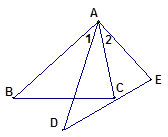
(1)求证:∆ABC∽∆ADE ;
(2)求AD的长。
(1)计算: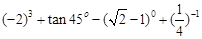
(2)(本小题5分)解不等式组: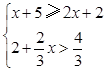
如图,在等腰梯形ABCD中,AB‖CD,已知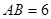 ,
,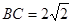 ,
,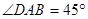 ,以
,以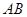 所在直线为
所在直线为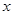 轴,
轴,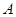 为坐标原点,建立直角坐标系,将等腰梯形ABCD绕A点按顺时针方向旋转
为坐标原点,建立直角坐标系,将等腰梯形ABCD绕A点按顺时针方向旋转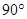 得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点)(如图).
得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点)(如图). 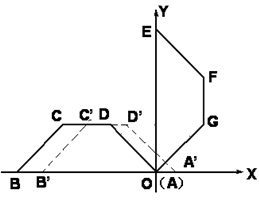
⑴在直线DC上是否存在一点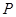 ,使
,使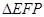 为等腰三角形,若存在,写出出
为等腰三角形,若存在,写出出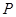 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
⑵将等腰梯形ABCD沿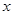 轴的正半轴平行移动,设移动后的
轴的正半轴平行移动,设移动后的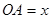 (0<x≤6),等腰梯形ABCD与等腰梯形OEFG重叠部分的面积为
(0<x≤6),等腰梯形ABCD与等腰梯形OEFG重叠部分的面积为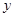 ,求
,求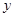 与
与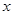 之间的函数关系式.并求出重叠部分的面积的最大值。
之间的函数关系式.并求出重叠部分的面积的最大值。