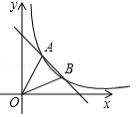
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于、两点,已知
(1)求一次函数和反比例函数的解析式;
(2)求点的坐标;
(3)连接、,求的面积.
计算题:
(1) 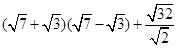
(2) 
如图,依次连结第一个正方形各边的中点得到第二个正方形,再依次连结第二个正方形各边的中点得到第三个正方形,按此方法继续下去。若第一个正方形边长为1,则第n个正方形的面积是.
平行四边形的一个角的平分线分对边为3和4两部分,则平行四边形的周长为.
如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作□ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F。
(1)当∠B=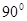 时,直接写出∠DEF的度数;
时,直接写出∠DEF的度数;
(2)在射线BM绕B点旋转的过程中,若∠B=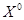 ,∠DEF=
,∠DEF=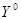 (
(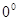 <X<
<X<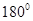 ,
,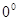 <Y<
<Y<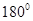 ),求:Y关于X的函数解析式及相应自变量X的取值范围,
),求:Y关于X的函数解析式及相应自变量X的取值范围,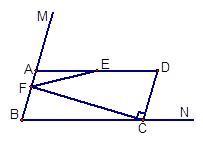
已知,△ABC中,∠BAC=45°,以AB边为边以点B为直角顶点在△ABC外部作等腰直角三角形ABD,以AC边为斜边在△ABC外部作等腰直角三角形ACE,连结BE、DC,两条线段相交于F,试求∠EFC的度数.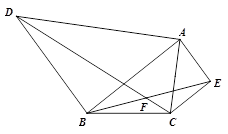
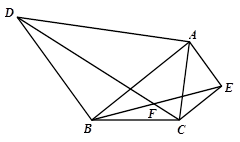
(备用图)