如图,已知直线与抛物线相交于点和点两点.
(1)求抛物线函数表达式;
(2)若点是位于直线上方抛物线上的一动点,以、为相邻的两边作平行四边形,当平行四边形的面积最大时,求此时平行四边形的面积及点的坐标;
(3)在抛物线的对称轴上是否存在定点,使抛物线上任意一点到点的距离等于到直线的距离?若存在,求出定点的坐标;若不存在,请说明理由.

建设中的昆石高速公路,在某施工段上沿AC方向开山修路,为加快施工速度,要在山坡的另一边同时施工,如图所示,从AC上的一点B取∠ABD=150°,BD=380米,∠D=60°,那么开挖点E离D多远,正好使A、C、E成一直线.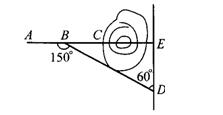
解不等式组 ;并写出它的整数解。
;并写出它的整数解。
已知 ,
,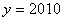 ,求代数式
,求代数式 的值。
的值。
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造如下正方形:
 |
再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、 …相应长方形的周长如下表所示:
| 序号 |
① |
② |
③ |
④ |
… |
| 周长 |
6 |
10 |
 |
 |
… |
仔细观察图形,上表中的 ,
, .
.
若按此规律继续作长方形,则序号为⑧的长方形周长是。
(9分)某商店打出了促销广告如下表.对顾客实行优惠,某人在此商场两次购物分别付款168元和423元.(1)第一次付款168元,可购价值多少元的货物?(2)第二次付款423元,可购价值多少元的货物?(3)若把两次的货物合在一次买,需要多少钱?
| 优惠条件 |
一次购物不超过200元 |
一次购物超过200元,但不超过500元 |
一次购物超过500元 |
| 优惠方法 |
不予优惠 |
按物价给予九折优惠 |
其中500元按九折优惠,超过500元部分按八折优惠. |