小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.
(一猜测探究
在中,,是平面内任意一点,将线段绕点按顺时针方向旋转与相等的角度,得到线段,连接.
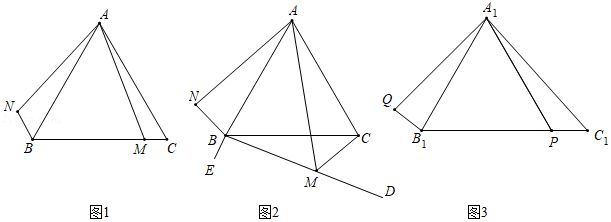
(1)如图1,若是线段上的任意一点,请直接写出与的数量关系是 ,与的数量关系是 ;
(2)如图2,点是延长线上点,若是内部射线上任意一点,连接,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
(二拓展应用
如图3,在△中,,,,是上的任意点,连接,将绕点按顺时针方向旋转,得到线段,连接.求线段长度的最小值.
如图,已知抛物线的对称轴是 轴,且点 , 在抛物线上,点 是抛物线上不与顶点 重合的一动点,过 作 轴于 , 轴于 ,延长 交抛物线于 ,设 是 关于抛物线顶点 的对称点, 是 点关于 的对称点.
(1)求抛物线的解析式及顶点 的坐标;
(2)求证:四边形 是平行四边形;
(3)求证:
,并求出当它们的相似比为
时的点
的坐标.
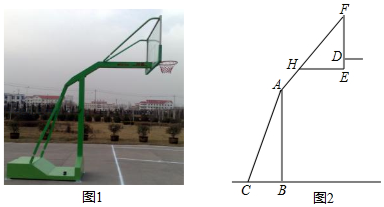
如图1,2分别是某款篮球架的实物图与示意图,已知底座 米,底座 与支架 所成的角 ,支架 的长为2.50米,篮板顶端 点到篮筐 的距离 米,篮板底部支架 与支架 所成的角 ,求篮筐 到地面的距离(精确到0.01米)(参考数据: , , , ,
收发微信红包已成为各类人群进行交流联系、增强感情的一部分,下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.
请问:(1)2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少?
(2)2017年六一甜甜和她妹妹各收到了多少钱的微信红包?

如图,已知 是 的直径, 与 相切于 , .
(1)求证: 是 的平分线;
(2)若 , 的半径 ,求 的长.

如图,已知反比例函数 的图象经过点 , 轴,且 的面积为2.
(1)求 和 的值;
(2)若点 也在反比例函数 的图象上,当 时,求函数值 的取值范围.
