阅读下面的材料:
如果函数满足:对于自变量的取值范围内的任意,,
(1)若,都有,则称是增函数;
(2)若,都有,则称是减函数.
例题:证明函数是减函数.
证明:设,
.
,
,.
.即.
.
函数是减函数.
根据以上材料,解答下面的问题:
已知函数,
,
(1)计算: , ;
(2)猜想:函数是 函数(填“增”或“减” ;
(3)请仿照例题证明你的猜想.
列方程或方程组解应用题:
为了进一步落实“北京市中小学课外活动计划”,某校计划用4000元购买乒乓球拍,用6000元购买羽毛球拍,且购买的乒乓球拍与羽毛球拍的数量相同.已知一副羽毛球拍比一副乒乓球拍贵40元,求一副乒乓球拍和一副羽毛球拍各是多少元.
已知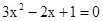 ,求代数式
,求代数式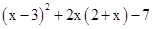 的值.
的值.
解不等式组: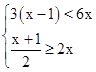
已知:如图,点E、C、D、A在同一条直线上,AB//DF,ED= AB,∠E=∠CPD.
求证:△ABC≌△DEF.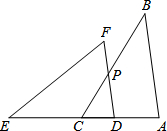
在平面直角坐标系xOy中,直线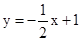 分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线
分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线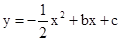 经过A,C两点,与
经过A,C两点,与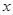 轴的另一交点为D.
轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线AB与CD的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,B,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.