汛期到来,山洪暴发.下表记录了某水库内水位的变化情况,其中表示时间(单位:,表示水位高度(单位:,当时,达到警戒水位,开始开闸放水.
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
14 |
15 |
16 |
17 |
18 |
14.4 |
12 |
10.3 |
9 |
8 |
7.2 |
(1)在给出的平面直角坐标系中,根据表格中的数据描出相应的点.
(2)请分别求出开闸放水前和放水后最符合表中数据的函数解析式.
(3)据估计,开闸放水后,水位的这种变化规律还会持续一段时间,预测何时水位达到.

请将式子: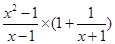 化简后,再选择一个合适的x的值代入求值.
化简后,再选择一个合适的x的值代入求值.
(1)计算:(-2011)0+(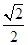 )-1+|
)-1+|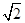 -2|-2cos60°;
-2|-2cos60°;
(2)解方程:(2x-1)2=x(3x+2)-7.
如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
如图,点C是半圆O的半径OB上的动点,作PC⊥AB于C.点D是半圆上位于PC左侧的点,连接BD交线段PC于E,且PD=PE.
(1)求证:PD是⊙O的切线;
(2)若⊙O的半径为4 ,PC=8
,PC=8 ,设OC=x,PD2=y.
,设OC=x,PD2=y.
①求y关于x的函数关系式;
②当x= 时,求tanB的值.
时,求tanB的值.
我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,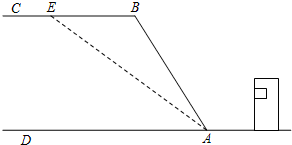
(1)求山坡高度;
(2)为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B 沿BC削进到E处,问BE至少是多少米(结果保留根号)?