为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表睡眠时间分布情况
组别 |
睡眠时间分组 |
人数(频数) |
1 |
||
2 |
11 |
|
3 |
||
4 |
4 |
请根据以上信息,解答下列问题:
(1) , , , ;
(2)抽取的这40名学生平均每天睡眠时间的中位数落在 组(填组别);
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于,请估计该校学生中睡眠时间符合要求的人数.

如图,在△ABC中,∠A=300, ,BC=
,BC= ,求AB的长。
,求AB的长。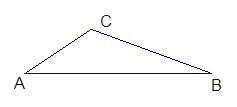
如图,抛物线与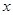 轴交于
轴交于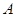 (
(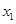 ,0)、
,0)、 (
( ,0)两点,且
,0)两点,且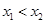 ,与
,与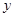 轴交于点
轴交于点 ,其中
,其中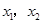 是方程
是方程 的两个根。
的两个根。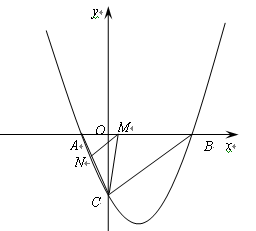
(1)求抛物线的解析式;
(2)点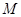 是线段
是线段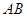 上的一个动点,过点
上的一个动点,过点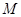 作
作 ∥
∥ ,交
,交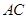 于点
于点 ,连接
,连接 ,当
,当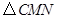 的面积最大时,求点
的面积最大时,求点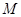 的坐标;
的坐标;
(3)点 在(1)中抛物线上,点
在(1)中抛物线上,点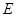 为抛物线上一动点,在
为抛物线上一动点,在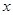 轴上是否存在点
轴上是否存在点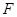 ,使以
,使以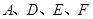 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点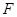 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
如图,已知Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连结BD。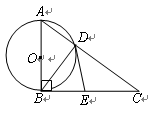
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连结DE,求证:ED与⊙O相切。
如图,为举办毕业联欢会,小颖设计了一个游戏:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘上的指针所指字母都相同时,他就获得一次指定一位到会者为大家表演节目的机会。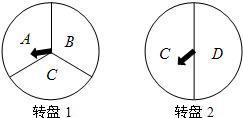
(1)利用树形图或列表的方法表示出游戏可能出现的所有结果。
(2)若小明参加一次游戏,则他能获得这种指定机会的概率是多少?
先阅读下面的例题,再按要求解答。
例:解一元二次不等式x2-9>0
解:∵x2-9=(x+3)(x-3) ∴(x+3)(x-3)>0
由有理数的乘法法则“两数相乘,同号得正”得
(1)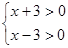 (2)
(2)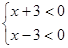
解不等式组(1),得x>3
解不等式组(2),得x<-3
∴(x+3)(x-3)>0的解集为x>3或x<-3
即一元二次不等式x2-9>0的解集为x>3或x<-3
问题:求分式不等式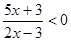 的解集
的解集