如图所示,已知正方形 的顶点 为正方形 对角线 、 的交点,连接 、 .
(1)求证: ;
(2)若 ,正方形 的边长为2,线段 与线段 相交于点 , ,求正方形 的边长.

如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A,B两点可构成直角三角形ABC,则称点C为A,B两点的勾股点.同样,点D也是A,B两点的勾股点.
(1)如图1,矩形ABCD中,AB=2,BC=1,请在边CD上作出A,B两点的勾股点(点C和点D除外)(要求:尺规作图,保留作图痕迹,不要求写作法);
(2)矩形ABCD中,AB=3,BC=1,直接写出边CD上A, B两点的勾股点的个数;
(3)如图2,矩形ABCD中,AB=12,BC=4,DP=4,DM=8,AN=5.过点P作直线l平行于BC,点H为M,N两点的勾股点,且点H在直线l上.求PH的长.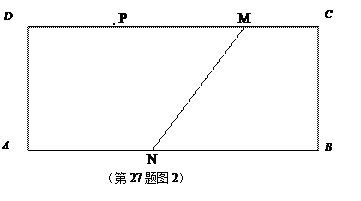
某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润(万元)与投资金额 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: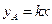 ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: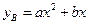 .根据公司信息部的报告,
.根据公司信息部的报告,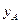 ,
,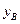 (万元)与投资金额
(万元)与投资金额 (万元)的部分对应值如下表所示:
(万元)的部分对应值如下表所示:
 |
1 |
5 |
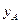 |
0.8 |
4 |
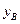 |
3.8 |
15 |
(1)填空: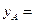 ;
;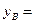 ;
;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为w(万元),试写出w与某种产品的投资金额x之间的函数关系式;
(3)请你设计一个在⑵中能获得最大利润的投资方案.
如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD交⊙O于点D,DE⊥BC,交BC的延长线于点E,BD交AC于点F.⑴求证:DE是⊙O的切线;(2) 若CE=1,ED=2,求⊙O的半径.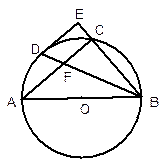
甲乙两人同时登山,甲、乙两人距地面的高度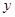 (米)与登山时间
(米)与登山时间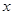 之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
之间的函数图象如图所示,根据图象所提供的信息解答下列问题: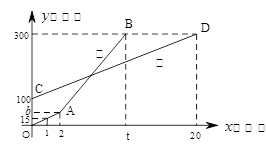
(1)甲登山的速度是每分钟米,乙在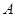 地提速时距地面的高度
地提速时距地面的高度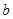 为 ____米;
为 ____米;
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度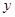 (米)与登山时间
(米)与登山时间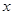 之间的函数关系式;
之间的函数关系式;
(3)登山多长时间时,乙追上了甲?
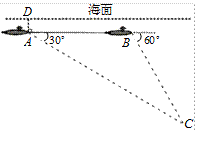
如图,一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度?(保留根号)