"互联网 "时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为 元 为正整数),每月的销售量为 条.
(1)直接写出 与 的函数关系式;
(2)设该网店每月获得的利润为 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
计算 .
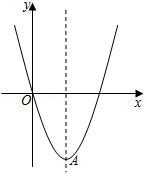
如图,在平面直角坐标系中,抛物线 经过原点 ,顶点为 .
(1)求抛物线的函数解析式;
(2)设点 为抛物线 的对称轴上的一点,点 在该抛物线上,当四边
形 为菱形时,求出点 的坐标;
(3)在(2)的条件下,抛物线 在第一象限的图象上是否存在一点 ,使得点 到直线 的距离与其到 轴的距离相等?若存在,求出直线 的函数解析式;若不存在,请说明理由.
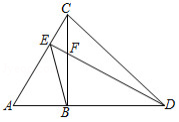
如图, 中, , 为 延长线上一点, ,过点 作 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)求 的度数;
(3)当 时,求 的值.
某商店销售一种商品,每件的进价为50元,经市场调研发现,当该商品每件的售价为60元时,每天可销售200件;当售价高于进价时,每件的售价每增加1元,每天的销售数量将减少10件.
(1)当每件商品的售价为64元时,求该商品每天的销售数量;
(2)当每件商品的售价为多少时,销售该商品每天获得的利润最大?并求出最大利润.
如图, 为 的直径, 为 上的一点, , , 的延长线交 于点 ,连接 .
(1)求证: 是 的切线;
(2)若 为 的中点,求 的值.
