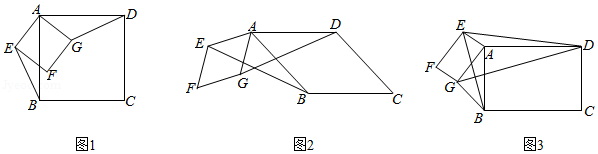
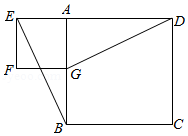
背景:一次小组合作探究课上,小明将两个正方形按如图所示的位置摆放(点 、 、 在同一条直线上),发现 且 .
小组讨论后,提出了下列三个问题,请你帮助解答:
(1)将正方形 绕点 按逆时针方向旋转(如图 ,还能得到 吗?若能,请给出证明;若不能,请说明理由;
(2)把背景中的正方形分别改成菱形 和菱形 ,将菱形 绕点 按顺时针方向旋转(如图 ,试问当 与 的大小满足怎样的关系时,背景中的结论 仍成立?请说明理由;
(3)把背景中的正方形分别改写成矩形 和矩形 ,且 , , ,将矩形 绕点 按顺时针方向旋转(如图 ,连接 , .小组发现:在旋转过程中, 的值是定值,请求出这个定值.
松鼠妈妈采松子,晴天每天可采20个,雨天每天可采12个,它一连几天采了112个松子,平均每天采14个,问这几天中有几天晴天,几天是雨天?
小明和小华在一起玩数字游戏,他们每人取了一张数字卡片,拼成了一个两位数.小明说:“哇!这个两位数的十位数字与个位数字之和恰好是9.”他们又把这两张卡片对调,得到了一个新的两位数,小华说:“这个两位数恰好也比原来的两位数大9.”
那么,你能回答以下问题吗?
(1)他们取出的两张卡片上的数字分别是几?
(2)第一次,他们拼出的两位数是多少?
(3)第二次,他们拼成的两位数又是多少呢?请你好好动动脑筋哟!
一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车.已知过去两次租用这两种货车的情况如下表:
| 第一次 |
第二次 |
|
| 甲种货车辆数(辆) |
2 |
5 |
| 乙种货车辆数(辆) |
3 |
6 |
| 累计运货吨数(吨) |
15.5 |
35 |
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?
一列快车长70米,慢车长80米,若两车同向而行,快车从追上慢车到完全离开慢车所用时间为20秒;若两车相向而行,则两车从相遇到离开时间为4秒,求两车每秒钟各行多少米?
如图:
若设快车每秒钟行x米,慢车每秒行y米.
根据题意填空:
(1)若同向而行,经过20秒快车行驶路程比慢车行驶路程多____米,可列方程_________.
(2)若相向而行,两车4秒钟共行驶__________米,可列方程__________________.
(3)由以上可得方程组__________________,解得________.
某汽车制造厂接受了在预定期限内生产一批汽车的任务,如果每天生产35辆,则差10辆才能完成任务;如果每天生产40辆,则可超额生产20辆.试求预定期限是多少天?计划生产多少辆汽车?
若设预定期限为x天,计划生产y辆汽车,请你根据题意填空,并列出方程组求x与y的值.
(1)若每天生产35辆,在预定期限x天内可生产__________辆,比计划产量y辆汽车__________(“多”或“少”)生产10辆,则可得二元一次方程______________________.
(2)若每天生产40辆,在预定期限x天内可生产__________辆,比计划产量y__________(填“多”或“少”)生产20辆,则可列二元一次方程_________________________.
(3)列方程组_________________________,并解得________.