如图,,为两个建筑物,两建筑物底部之间的水平地面上有一点,从建筑物的顶点测得点的俯角为,从建筑物的顶点测得点的俯角为,测得建筑物的顶点的俯角为.若已知建筑物的高度为20米,求两建筑物顶点、之间的距离(结果精确到,参考数据:,.

解方程:(1)x2+x―12=0;
如图,BD平分∠ABC,且AB=4,BC=6,则当BD=时,△ABD∽△DBC.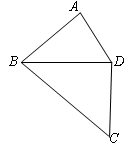
已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=mx+n(m≠0)的图象相交于点A(―2,4),B(8,2),如图所示,则能使y1<y2成立的x的取值范围是.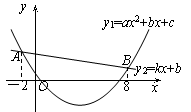
如图,已 知直线 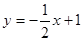 交坐标轴于
交坐标轴于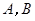 两点,以线段
两点,以线段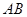 为边向上作正方形
为边向上作正方形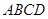 ,过点
,过点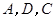 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为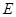 .
.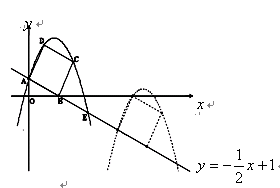
(1)请直接写出点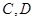 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒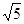 个单位长度的速度沿射线
个单位长度的速度沿射线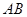 下滑,直至顶点
下滑,直至顶点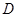 落在x轴上时停止.设正方形落在
落在x轴上时停止.设正方形落在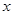 轴下方部分的面积为
轴下方部分的面积为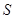 ,求
,求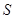 关于滑行时间
关于滑行时间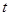 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量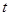 的取值范围;
的取值范围;
(4)在(3)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上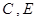 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.
有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长
保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位
个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,
此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,
平均每天还有1千克葡萄变质丢弃.
(1)设5天后每千克鲜葡萄的市场价为P元,则P=;
(2)若存放x天后将鲜葡萄一次性出售,销售金额为760元,求x的值 ? (3)问个体户将这批葡萄存放多少天后出售,可获得最大利润?最大利润Q是多少?