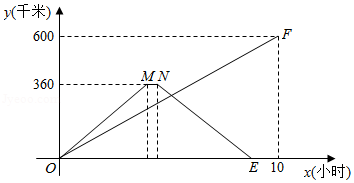
在一条公路上依次有，，三地，甲车从地出发，驶向地，同时乙车从地出发驶向地，到达地停留0.5小时后，按原路原速返回地，两车匀速行驶，甲车比乙车晚1.5小时到达地．两车距各自出发地的路程（千米）与时间（小时）之间的函数关系如图所示．请结合图象信息答案下列问题：
（1）甲车行驶速度是 千米1时，，两地的路程为 千米；
（2）求乙车从地返回地的过程中，（千米）与（小时）之间的函数关系式（不需要写出自变量的取值范围）；
（3）出发多少小时，行驶中的两车之间的路程是15千米？请你直接写出答案．
在下图中，每个正方形由边长为1 的小正方形组成：
| 正方形边长 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
| 黑色小正方形个数 |
1 |
4 |
5 |
8 |
（1）观察图形，请填写下列表格；
（2）在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1，白色小正方形的个数
为P2，问是否存在偶数n，使P2="5" P1?若存在，请求出n的值；若不存在，请说明理由．
定义：如图1，点C在线段AB上，若满足AC2=BC•AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．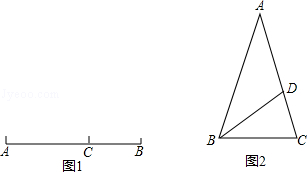
（1）求证：点D是线段AC的黄金分割点；
（2）求出线段AD的长．
已知：如图， AB是⊙O的直径，点C、D为圆上两点，且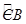
=
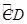，CF⊥AB于点F，CE⊥AD的延长线于点E．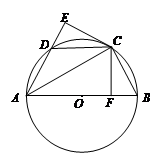
（1）试说明：DE＝BF；
（2）若∠DAB＝60°，AB＝8，求△ACD的面积．
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B
（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6
，AF=4，求AE的长．
如图，在方格纸上，△ABC与△A1B1C1是关于点O为位似中心的位似图形，它们的顶点都在格点上．
（1）画出位似中心O；
（2）求出△ABC与△A1B1C1的位似比；
（3）以O点为位似中心，再画一个△A2B2C2使它与△ABC的位似比等于3．