如图1,抛物线与抛物线相交轴于点,抛物线与轴交于、两点(点在点的右侧),直线交轴负半轴于点,交轴于点,且.
(1)求抛物线的解析式与的值;
(2)抛物线的对称轴交轴于点,连接,在轴上方的对称轴上找一点,使以点,,为顶点的三角形与相似,求出的长;
(3)如图2,过抛物线上的动点作轴于点,交直线于点,若点是点关于直线的对称点,是否存在点(不与点重合),使点落在轴上?若存在,请直接写出点的横坐标,若不存在,请说明理由.

已知关于x的方程 的两根是一个矩形两邻边的长.
的两根是一个矩形两邻边的长.
(1)k取何值时,方程在两个实数根;
(2)当矩形的对角线长为 时,求k的值.
时,求k的值.
如图,要利用一面墙(墙长为25米)建羊圈,用75米的围栏围成总面积为300平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?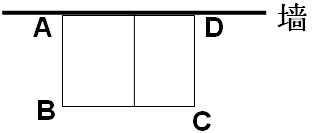
已知,如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且DE平分∠CDF.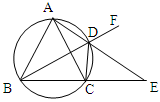
(1)求证:AB=AC;
(2)若AC=3cm,AD=2cm,求DE的长.
如图所示, 是圆O的一条弦,
是圆O的一条弦, ,垂足为
,垂足为 ,交圆O于点
,交圆O于点 ,点
,点 在圆O上.
在圆O上.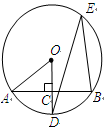
(1)若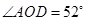 ,求
,求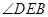 的度数;
的度数;
(2)若AC= ,CD=1,求圆O的半径.
,CD=1,求圆O的半径.
如图,在平面直角坐标系中,O为原点,每个小方格的边长为1个单位长度.在第一象限内有横、纵坐标均为整数的A、B两点,且OA= OB=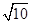 .
.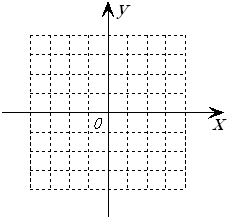
(1)写出A、B两点的坐标;
(2)将线段AB绕点O旋转一周,求所形成的图形的面积(结果保留π).