2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数(人与时间(分钟)的变化情况,数据如下表:(表中表示
时间(分钟) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
人数(人 |
0 |
170 |
320 |
450 |
560 |
650 |
720 |
770 |
800 |
810 |
810 |
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出与之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?
计算:
(1)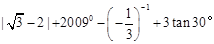
(2)先化简,再求值: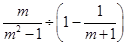 ,其中
,其中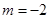
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3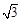 ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,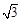 ,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
请解答下列问题:过A,B两点的直线解析式是▲
当t﹦4时,点P的坐标为▲ ;当t ﹦▲,点P与点E重合;
① 作点P关于直线EF的对称点P′. 在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?
② 当t﹦2时,是否存在着点Q,使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标;若不存在,请说明理由.
一辆客车从甲地开往甲地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示: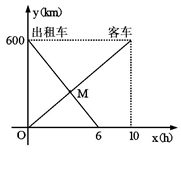
根据图象,直接写出y1,y2关于x的函数关系式
分别求出当x=3,x=5,x=8时,两车之间的距离。
若设两车间的距离为S(km),请写出S关于x的函数关系式
甲、乙两地间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油。求出A加油站到甲地的距离。
某地建成跨海大桥通车后,A地到B港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时求A地经跨海大桥到B港的路程
若货物运输费用包括运输成本和时间成本,已知某车货物从A地到B港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经跨海大桥到B港的运输费用是多少元?
A地准备开辟向C城方向的外运路线,即货物从A地跨海大桥到B港,再从B港运到C地.若有一批货物(不超过10车)从A地按外运路线运到C地的运费需8320元,其中从A地经跨海大桥到B港的每车运输费用与(2)中相同,从B港到C地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.求新传送带AC的长度;
如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:
 ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.24,
≈2.24, ≈2.45)
≈2.45)