如图，AB是⊙O的直径，C为⊙O上一点，连接AC，CE⊥AB-优题课

游客

题文

如图， $AB$ 是 $⊙ O$ 的直径， $C$ 为 $⊙ O$ 上一点，连接 $AC$ ， $CE ⊥ AB$ 于点 $E$ ， $D$ 是直径 $AB$ 延长线上一点，且 $∠ BCE = ∠ BCD$ ．

（1）求证： $CD$ 是 $⊙ O$ 的切线；

（2）若 $AD = 8$ ， $\frac{BE}{CE} = \frac{1}{2}$ ，求 $CD$ 的长．

科目数学题型解答题难度中等

知识点：解直角三角形相似三角形的判定与性质切线的判定与性质

登录免费查看答案和解析

相关试题

如图（1），把一张顶角为36°的等腰三角形纸片剪两刀，分成三张小纸片，使每张小纸片都是等腰三角形．定义：如过两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
尺规作图（保留痕迹，不写作法）：请在图（2）中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数（若两种方法分得的三角形成3对全等三角形，则视为同一种）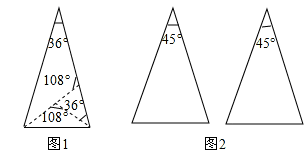

如图，均匀的正四面体的各面依次标有1，2，3，4四个数字．小明做了60次投掷试验，结果统计如下：

（1）计算上述试验中“4朝下”的频率是__________；
（2）“根据试验结果，投掷一次正四面体，出现2朝下的概率是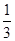．”的说法正确吗？为什么？
（3）随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．

如图，抛物线y=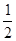x²＋bx＋c与y轴交于点C（0，－4），与x轴交于点A，B，且B点的坐标为（2，0）

（1）求该抛物线的解析式．
（2）若点P是AB上的一动点，过点P作PE∥AC，交BC于E，连接CP，求△PCE面积的最大值．
（3）若点D为OA的中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．

已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．

（1）求证：DE是⊙O的切线；
（2）若DE=6cm，AE=3cm，求⊙O的半径．

如图，小明想测山高和索道的长度．他在B处仰望山顶A，测得仰角∠B=31°，再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE=39°．

（1）求这座山的高度（小明的身高忽略不计）；
（2）求索道AC的长（结果精确到0．1m）．
（参考数据：tan31°≈，sin31°≈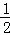，tan39°≈，sin39°≈）

试卷网试题网古诗词网作文网范文网