如图,反比例函数 的图象与正比例函数 的图象相交于 、 两点,点 在第四象限, 轴.
(1)求 的值;
(2)以 、 为边作菱形 ,求 点坐标.
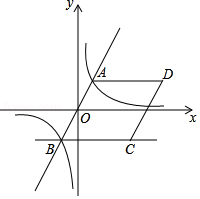
如图,在平面直角坐标系中,二次函数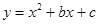 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(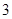 ,
, ),与y轴交于C(
),与y轴交于C( ,
,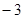 )点,点P是直线BC下方的抛物线上一动点.
)点,点P是直线BC下方的抛物线上一动点.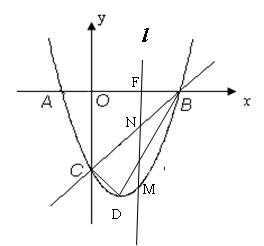
(1)求这个二次函数的解析式;
(2)若抛物线的顶点为点D,求△BCD的面积;
(3)设M是(1)所得抛物线上第四象限内的一个动点,过点M作直线l⊥x 轴于点F,交直线BC于点N。试问:线段MN的长度是否存在最大值?若存在,求出它最大值及此时M点的坐标;若不存在,请说明理由.
已知,如图,在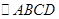 中,AE⊥BC,垂足为E,点F为CE上的一点,点G为CD上的一点,CF=CG,连接DF、EG、AG, AG=EG,∠1=∠2.
中,AE⊥BC,垂足为E,点F为CE上的一点,点G为CD上的一点,CF=CG,连接DF、EG、AG, AG=EG,∠1=∠2.
(1)若CE=4,AE=3,求BE的长;
(2)求证:∠CEG=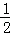 ∠AGE.
∠AGE.
某蔬菜店第一次用800元购进某种蔬菜,由于销售状况良好,该店又用了1400元第二次购进该种蔬菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元。
(1)第一次所购的该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,并且忽略其他因素,要使该蔬菜店售完这些蔬菜获利不低于1700元,则该蔬菜每千克售价至少为多少?
某中学九(1)班为了了解全班学生喜欢球类活动的情况,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),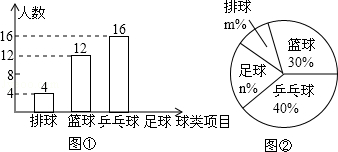
请你根据图中提供的信息解答下列问题:各个兴趣小组人数统计图各个兴趣小组总人数占调查人数百分比统计图
(1)九(1)班的学生人数为,并把条形统计图补充完整;
(2)扇形统计图中m=,n=,表示“足球”的扇形的圆心角是度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
 先化简,再求值:
先化简,再求值: ,其中
,其中 是方程
是方程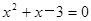 的解.
的解.