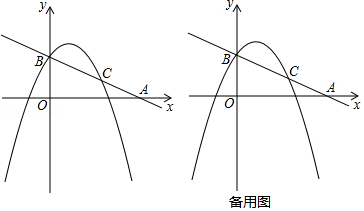
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 过点 且与直线相交于另一点 , .
(1)求抛物线的解析式;
(2)点 是抛物线上的一动点,当 时,求点 的坐标;
(3)点 , 在 轴的正半轴上,点 是 轴正半轴上的一动点,且满足 .
①求 与 之间的函数关系式;
②当 在什么范围时,符合条件的 点的个数有2个?
已知函数 ,当 时, 的最小值为 ,最大值为 ,求 的值.
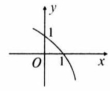
已知二次函数 的图象的一部分如图所示,试确定 的取值范围.
已知二次函数 及实数 .求:
(1)函数在 的最小值;
(2)函数在 的最小值.
已知抛物线 经过点 ,当 时, 随 的增大而增大,当 时, 随 的增大而减小.设 是抛物线 与 轴的交点(交点也称公共点)的横坐标, .
(1)求 的值;
(2)求证: ;
(3)以下结论: ,你认为哪个正确?请证明你认为正确的那个结论.
在平面直角坐标系 中,抛物线 与 轴交于 两点.
(1)求抛物线的解析式及点 的坐标;
(2)当 时的函数图象记为 ,求此时函数 的取值范围;
(3)在(2)的条件下,将图象 在 轴上方的部分沿 轴翻折,图象 的其余部分保持不变,得到一个新图象 .若经过 点的直线 与图象 在第三象限内有两个公共点,结合图象,求 的取值范围.