如图1，在等腰直角三角形 中， ， ．点 是 的中点，以 为边作正方形 ，连接 ， ．将正方形 绕点 顺时针旋转，旋转角为 ．
（1）如图2，在旋转过程中，
①判断 与 是否全等，并说明理由；
②当 时， 与 交于点 ，求 的长．
（2）如图3，延长 交直线 于点 ．
①求证： ；
②在旋转过程中，线段 的长度是否存在最大值？若存在，求出最大值；若不存在，请说明理由．
已知一次函数y=kx+b的图象经过点（1，3）和点（2，5），求k和b的值．
如图，已知△ABC．
（1）作边BC的垂直平分线；
（2）作∠C的平分线．（要求：不写作法，保留作图痕迹）
①计算：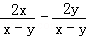
②解方程：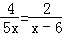
．
（1）如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得线段BE、EF、FD之间的数量关系为．
（2）如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF=
∠BAD，线段BE、EF、FD之间存在什么数量关系，为什么？
（3）如图3，点A在点O的北偏西30°处，点B在点O的南偏东70°处，且AO=BO，点A沿正东方向移动249米到达E处，点B沿北偏东50°方向移动334米到达点F处，从点O观测到E、F之间的夹角为70°，根据（2）的结论求E、F之间的距离．
在正方形ABCD中，AB=4．
（1）正方形ABCD的周长为；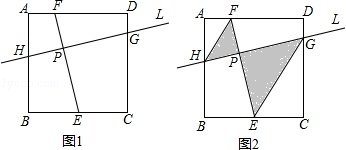
（2）如图1，点E、F分别在BC和AD上，点P是线段EF上的动点，过点P作EF的垂线L，若直线L与正方形CD、AB的交点分别在G、H．
①求证：EF=GH；
②已知，BE=2，AF=1，若线段PE的长度为a，求a的最小值；
③如图2，在②的条件下，已知AH=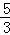
，PE=2PF，求图中阴影部分的面积．