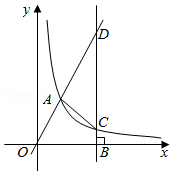
如图,正比例函数的图象与反比例函数的图象交于点.点为轴正半轴上一点,过作轴的垂线交反比例函数的图象于点,交正比例函数的图象于点.
(1)求的值及正比例函数的表达式;
(2)若,求的面积.
如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),与 轴交于点 .
(1)试探究 的外接圆的圆心位置,求出圆心坐标;
(2)点 是抛物线上一点(不与点 重合),且 ,求 的度数;
(3)在(2)的条件下,点 是 轴上方抛物线上一点,点 是抛物线对称轴上一点,是否存在这样的点 和点 ,使得以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.

如图, ,点 是 平分线上的一点,过点 分别作 , ,垂足分别为点 , , ,点 为线段 上的一点(点 不与点 、 重合),连接 ,以 为直角边,点 为直角顶点,作等腰直角三角形 ,点 落在 左侧.
(1)求证: ;
(2)连接 ,请你判断 与 的位置关系,并说明理由;
(3)设 , 的面积为 ,求 与 之间的函数关系式.
如图,一次函数 的图象交 轴于点 、交 轴于点 , 的平分线交 轴于点 ,过点 作直线 ,垂足为点 ,交 轴于点 .
(1)求直线 的解析式;
(2)在线段 上有一动点 (不与点 , 重合),过点 分别作 轴, 轴,垂足为点 、 ,是否存在点 ,使线段 的长最小?若存在,请直接写出点 的坐标;若不存在,请说明理由.

某网络经销商销售一款夏季时装,进价每件60元,售价每件130元,每天销售30件,每销售一件需缴纳网络平台管理费4元.未来30天,这款时装将开展“每天降价1元”的促销活动,即从第一天起每天的单价均比前一天降1元,通过市场调查发现,该时装单价每降1元,每天销售量增加5件,设第 天 且 为整数)的销量为 件.
(1)直接写出 与 的函数关系式;
(2)在这30天内,哪一天的利润是6300元?
(3)设第 天的利润为 元,试求出 与 之间的函数关系式,并求出哪一天的利润最大,最大利润是多少.
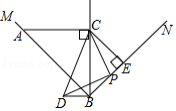
如图, , 均为直角三角形, , , 与 相交于点 ,以 为直径的 恰好经过点 ,并与 , 分别交于点 和点 .
(1)求证: .
(2)若 , ,求 的长.
