如图,二次函数的图象与轴交于点,过点作轴的平行线交抛物线于另一点,抛物线过点,且顶点为,连接、、、.
(1)填空: ;
(2)点是抛物线上一点,点的横坐标大于1,直线交直线于点.若,求点的坐标;
(3)点在直线上,点关于直线对称的点为,点关于直线对称的点为,连接.当点在轴上时,直接写出的长.

在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=600mm,求油的最大深度.
先阅读,后回答问题:x为何值时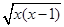 有意义?
有意义?
解:要使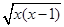 有意义需
有意义需 ≥0,
≥0,
由乘法法则得:  或
或 ,
,
解之得:x≥1 或x≤0,
即当x≥1 或x≤0时,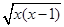 有意义。
有意义。
体会解题思想后,解答,x为何值是 有意义?
有意义?
经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A、B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
(1)若质量为(5±0.25)kg的为优等品,根据以上信息完成下表:
| 优等品数量(颗) |
平均数 |
方差 |
|
| A |
5.0 |
0.103 |
|
| B |
5.0 |
0.093 |
(2)请分别从优等品数量、平均数与方差三方面对A、B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为(3,2)、(1,3).△AOB绕点O逆时针旋转90º后得到△A1OB1.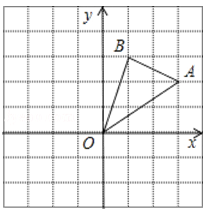
(1)在网格中画出△A1OB1,并标上字母;
(2)点A关于O点中心对称的点的坐标为 ;
(3)点A1的坐标为 ;
(4)在旋转过程中,点B经过的路径为弧BB1,那么弧BB1的长为 .
解方程:
(1)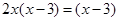
(2)