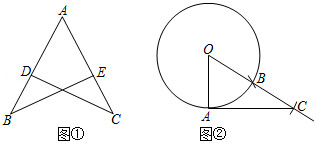
(1)如图①,点 在 上,点 在 上, , .求证: .
(2)如图②, 为 上一点,按以下步骤作图:
①连接 ;
②以点 为圆心, 长为半径作弧,交 于点 ;
③在射线 上截取 ;
④连接 .
若 ,求 的半径.
求不等式组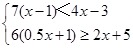 的整数解.
的整数解.
如图,二次函数y= x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP= S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ≈1.414.
≈1.414. ≈1.732)
≈1.732)
某校选派一部分学生参加“六盘水市马拉松比赛”,要为每位参赛学生购买一顶帽子.商场规定:凡一次性购买200顶或200顶以上,可按批发价付款;购买200顶以下只能按零售价付款.如果为每位参赛学生购买1顶,那么只能按零售价付款,需用900元;如果多购买45顶,那么可以按批发价付款,同样需用900元.问:
(1)参赛学生人数x在什么范围内?
(2)若按批发价购买15顶与按零售价购买12顶的款相同,那么参赛学生人数x是多少?
(1)三角形内角和等于 .
(2)请证明以上命题.