在平面直角坐标系中,抛物线 经过点 和点 ,与 轴交于点 ,与 轴的另一交点为点 .
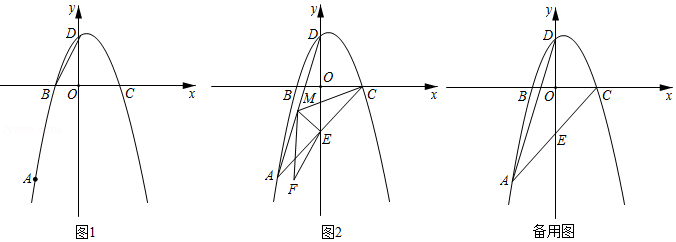
(1)求抛物线的解析式;
(2)如图1,连接 ,在抛物线上是否存在点 ,使得 ?若存在,请求出点 的坐标;若不存在,请说明理由;
(3)如图2,连接 ,交 轴于点 ,点 是线段 上的动点(不与点 ,点 重合),将 沿 所在直线翻折,得到 ,当 与 重叠部分的面积是 面积的 时,请直接写出线段 的长.
a、b、c在数轴上的位置如图所示:
化简:|a|-|a+b|+|c-a|+|b-c|
股民李星星在上周星期五以每股11.2元买了一批股票,下表为本周星期一到星期五该股票的涨跌情况
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌/元 |
+0.4 |
+0.45 |
-0.2 |
+0.25 |
-0.4 |
求:(1)本周星期三收盘时,每股的钱数.(5分)
(2)李星星本周内哪一天把股票抛出比较合算,为什么?(5分)
某市出租车的收费标准为:起步价10元,可行3千米(包括3千米),超过3千米的部分每千米1.4元。
(1)若小张坐出租车6千米,要付费多少元?(4分)
(2)他乘坐出租车x千米(x>3),付费多少元?(4分)
若a、b互为相反数,c、d互为倒数,且m=-4,
(1)a+b=__________(2分)
(2)cd=__________(2分)
(3)求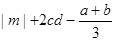 的值.(5分)
的值.(5分)
当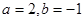 时,求代数式
时,求代数式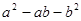 的值
的值